题目内容
(文)数列{an}中a1=0,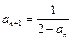 ,(1)求证数列
,(1)求证数列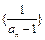 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设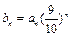 ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有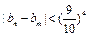 .
.
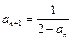 ,(1)求证数列
,(1)求证数列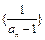 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设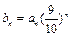 ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有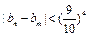 .
.(1)略 (2)略
(1)∵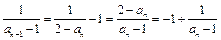 即
即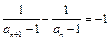 ,∴公差d=-1.
,∴公差d=-1.
且首项为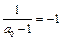 ,故
,故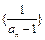 是等差数列.
是等差数列.
(2)∵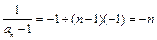 ,∴
,∴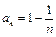 .
.
设f(x)=x-ln(x+1),(x>0),则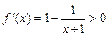 ,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴
,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴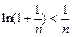 ,即
,即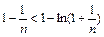 .
.
∴an<1-ln(n+1)+lnn,∴Sn<(1-ln2+ln1)+(1-ln3+ln2)+…+[1-ln(n+1)+lnn]=n-ln(n+1)故Sn<n-ln(n+1).
(3)∵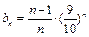 ,∴
,∴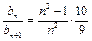 ,当
,当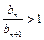 时,则
时,则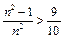 ,∴
,∴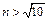 ,
,
即n≥4;又当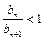 时,则
时,则 ,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有
,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有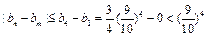
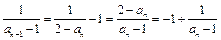 即
即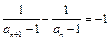 ,∴公差d=-1.
,∴公差d=-1.且首项为
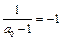 ,故
,故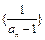 是等差数列.
是等差数列.(2)∵
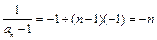 ,∴
,∴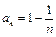 .
.设f(x)=x-ln(x+1),(x>0),则
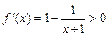 ,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴
,f(x)在(0,+∞)↑,且f(x)在[0,+∞)上连续,∴f(x)>f(0)=0,∴x>0时x>ln(x+1), ∴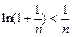 ,即
,即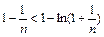 .
.∴an<1-ln(n+1)+lnn,∴Sn<(1-ln2+ln1)+(1-ln3+ln2)+…+[1-ln(n+1)+lnn]=n-ln(n+1)故Sn<n-ln(n+1).
(3)∵
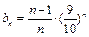 ,∴
,∴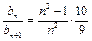 ,当
,当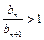 时,则
时,则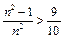 ,∴
,∴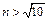 ,
,即n≥4;又当
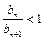 时,则
时,则 ,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有
,即n≤3,因此得b1<b2<b3<b4>b5>b6>…,又∵b1=0,n≥2时,bn>0,∴0≤bn≤b4.∴对任意正整数n、m,都有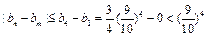

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
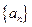 中,
中,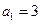 ,
,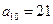 ,通项
,通项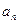 是项数
是项数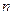 的一次函数,
的一次函数,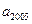 ;
;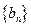 是由
是由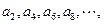 组成,试归纳
组成,试归纳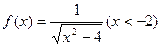 .
.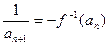 (nÎN+),求{an}的通项公式an;
(nÎN+),求{an}的通项公式an;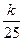 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.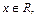 记不超过
记不超过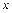 的最大整数为[
的最大整数为[ {
{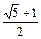 },[
},[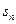 ,若
,若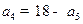 ,则
,则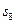 =
= 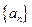 是公比为
是公比为 的等比数列,
的等比数列,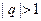 ,令
,令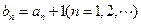 ,若数列
,若数列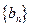 有连续四项在集合
有连续四项在集合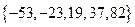 中,则
中,则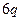 = ▲ .
= ▲ .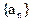 是等和数列且
是等和数列且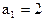 ,公和为5,那么
,公和为5,那么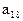 的值为_______,且这个数列前21项和
的值为_______,且这个数列前21项和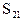 的值为_______。
的值为_______。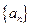 的前
的前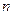 项和为
项和为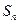 ,若
,若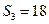 ,则
,则