题目内容
13.已知函数f(x)为一次函数,且单调递增,满足f[f(x)]=$\frac{1}{4}$x-$\frac{3}{4}$,若对于数列{an}满足:a1=-1,a2=2,an+1=4f(an)-an-1+4(n≥2).(Ⅰ)试求数列{an}的通项公式;
(Ⅱ)设bn=$\frac{{a}_{n}+2}{n}$×($\frac{1}{2}$)n-1,数列{bn}的前n项的和为Sn求证:Sn<4.
分析 (Ⅰ)设出一次函数解析式,由f[f(x)]=$\frac{1}{4}$x-$\frac{3}{4}$求得函数解析式,代入an+1=4f(an)-an-1+4(n≥2)得到数列递推式,然后构造等差数列{an+1-an},求其通项公式后,利用累加法求数列{an}的通项公式;
(Ⅱ)把数列{an}的通项公式代入bn=$\frac{{a}_{n}+2}{n}$×($\frac{1}{2}$)n-1,然后利用错位相减法求数列{bn}的前n项的和为Sn,即可证明Sn<4.
解答 (Ⅰ)解:∵f(x)为一次函数,且单调递增,
∴设f(x)=kx+b(k>0),
则由f[f(x)]=$\frac{1}{4}$x-$\frac{3}{4}$,得$k(kx+b)+b={k}^{2}x+kb+b=\frac{1}{4}x-\frac{3}{4}$,
∴$\left\{\begin{array}{l}{{k}^{2}=\frac{1}{4}}\\{kb+b=-\frac{3}{4}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$.
∴f(x)=$\frac{1}{2}x-\frac{1}{2}$.
则an+1=4f(an)-an-1+4=$4(\frac{1}{2}{a}_{n}-\frac{1}{2})-{a}_{n-1}+4$=2an-an-1+2(n≥2).
即(an+1-an)-(an-an-1)=2,
∵a1=-1,a2=2,∴a2-a1=3,
∴数列{an+1-an}构成以3为首项,以2为公差的等差数列,
则an+1-an=3+2(n-1)=2n+1.
∴a2-a1=2×1+1,
a3-a2=2×2+1,
…
an-an-1=2(n-1)+1(n≥2).
累加得:an=a1+2[1+2+…+(n-1)]+(n-1)=$-1+2×\frac{n(n-1)}{2}+(n-1)={n}^{2}-2$.
验证n=1时上式成立,
∴${a}_{n}={n}^{2}-2$;
(Ⅱ)证明:bn=$\frac{{a}_{n}+2}{n}$×($\frac{1}{2}$)n-1=$\frac{{n}^{2}-2+2}{n}×(\frac{1}{2})^{n-1}=n×(\frac{1}{2})^{n-1}$,
则Sn=b1+b2+…+bn=$1×(\frac{1}{2})^{0}+2×(\frac{1}{2})^{1}+3×(\frac{1}{2})^{2}+…+$$n×(\frac{1}{2})^{n-1}$,
$\frac{1}{2}{S}_{n}=1×(\frac{1}{2})^{1}+2×(\frac{1}{2})^{2}+3×(\frac{1}{2})^{3}$$+…+n×(\frac{1}{2})^{n}$.
两式作差得:$\frac{1}{2}{S}_{n}=1+\frac{1}{2}+(\frac{1}{2})^{2}+…+(\frac{1}{2})^{n-1}-n×(\frac{1}{2})^{n}$=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}-n×(\frac{1}{2})^{n}$=$2-(\frac{1}{2})^{n-1}-n×(\frac{1}{2})^{n}$.
∴${S}_{n}=4-(\frac{1}{2})^{n}-n×(\frac{1}{2})^{n+1}<4$.
点评 本题考查数列的函数特性,考查了等差数列的确定,训练了累加法求数列的通项公式,训练了错位相减法求数列的前n项和,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
| A. | 周期为2π的奇函数 | B. | 周期为$\frac{π}{2}$的奇函数 | ||
| C. | 周期为π的偶函数 | D. | 周期为2π的偶函数 |
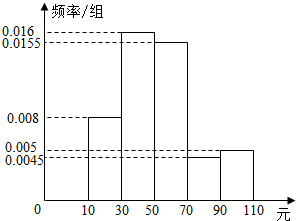 一家电信公司在某大学对学生每月的手机话费进行抽样调查,随机抽取了100名学生,将他们的手机话费情况进行统计分析,绘制成频率分布直方图(如图所示).如果该校有大学生10000人,请估计该校每月手机话费在[50,70)的学生人数是3100.
一家电信公司在某大学对学生每月的手机话费进行抽样调查,随机抽取了100名学生,将他们的手机话费情况进行统计分析,绘制成频率分布直方图(如图所示).如果该校有大学生10000人,请估计该校每月手机话费在[50,70)的学生人数是3100.