题目内容
【题目】已知函数f（x）=﹣3x2+a（6﹣a）x+c．
（1）当c=19时，解关于a的不等式f（1）＞0；
（2）若关于x的不等式f（x）＞0的解集是（﹣1，3），求实数a，c的值．
【答案】
（1）解：c=19时，f（1）=﹣3+6a﹣a2+19=﹣a2+6a+16＞0，
化为a2﹣6a﹣16＜0，解得﹣2＜a＜8．
∴不等式的解集为（﹣2，8）
（2）解：由已知有﹣1，3是关于x的方程3x2﹣a（6﹣a）x﹣c=0的两个根，
则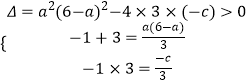 
，
解得 
【解析】（1）c=19时，f（1）=﹣3+6a﹣a2+19=﹣a2+6a+16＞0，化为a2﹣6a﹣16＜0，解得即可；（2）利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可得出．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减，以及对解一元二次不等式的理解，了解求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．
练习册系列答案
相关题目
