题目内容
7.若不等式x2-ax+a≤1有解,则a的取值范围为( )| A. | a<2 | B. | a=2 | C. | a>2 | D. | a∈R |
分析 不等式x2-ax+a≤1有解,即b2-4ac≥0即可,从而求出a的取值范围.
解答 解:∵不等式x2-ax+a≤1有解,
∴x2-ax+a-1≤0,
∴△=a2-4(a-1)≥0,
即a2-4a+4≥0,
即(a-2)2≥0,
解得a∈R,
故选:D
点评 本题考查了二次函数与不等式的解法与应用问题,是基础题.

练习册系列答案
相关题目
17.已知直线y=kx+1与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点,则实数m的取值范围为( )
| A. | m≥1 | B. | m≥1或0<m<1 | C. | m≥1且m≠5 | D. | 0<m<5且m≠1 |
12.已知等比数列{an}的公比为正数,且a3•a9=2a52,a2=2,则a1的值是( )
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
19.设$a={(\frac{2}{3})^x}$,$b={(\frac{3}{2})^{x-1}}$,$c={log_{\frac{2}{3}}}x$,若x>1,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
16.某公司招聘员工,初试设置计算机、礼仪、专业技能、基本素质共四个科目的考试,要求专业技能、基本素质都要合格,且计算机、礼仪至少有一门合格,则能取得参加复试的资格,现有甲、乙、丙三个人参加初试,每一个人对这四门考试是否合格相互独立,其合格的概率均相同(见表),且每一门课程是否合格相互独立.
(1)求乙取得参加复试的资格的概率;
(2)记ξ表示三个人中取得复试的资格的人数,求ξ的分布及期望Eξ.
| 科目 | 基本素质 | 专业技能 | 计算机 | 礼仪 |
| 合格的概率 | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
(2)记ξ表示三个人中取得复试的资格的人数,求ξ的分布及期望Eξ.
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
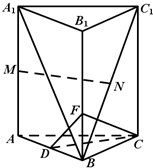 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.