题目内容
2.已知tanα=$\frac{2}{5}$,tanβ=$\frac{1}{4}$,则tan(α-β)等于( )| A. | $\frac{13}{18}$ | B. | $\frac{13}{22}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{22}$ |
分析 直接利用两角差的正切函数化简求解即可.
解答 解:tanα=$\frac{2}{5}$,tanβ=$\frac{1}{4}$,
则tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{\frac{2}{5}-\frac{1}{4}}{1+\frac{2}{5}×\frac{1}{4}}$=$\frac{3}{22}$.
故选:D.
点评 本题考查两角差的正切函数的应用,基本知识的考查.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
12.已知等比数列{an}的公比为正数,且a3•a9=2a52,a2=2,则a1的值是( )
| A. | $±\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
13.已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)与直线y=b相交于A、B两点,O是坐标原点,如果△AOB是等边三角形,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
14.设集合A={x|x2+3x<0},B={x|x<-1},则A∩B=( )
| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|x<-1} | D. | {x|x>0} |
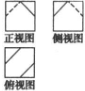 一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.