题目内容
5.已知f(x)是R上的奇函数,且当x∈(-∞,0]时,f(x)=-xlg(2m-x+$\frac{1}{2}$).当x>0时,不等式f(x)<0恒成立,则m的取值范围是( )| A. | (-∞,-1) | B. | (-1,1] | C. | [0,+∞) | D. | [-1,+∞) |
分析 由题意,当x∈(-∞,0)时,f(x)=-xlg(2m-x+$\frac{1}{2}$)>0恒成立;从而化为最值问题,从而解得.
解答 解:∵f(x)是R上的奇函数,
又∵当x>0时,不等式f(x)<0恒成立,
∴当x∈(-∞,0)时,f(x)=-xlg(2m-x+$\frac{1}{2}$)>0恒成立;
∴2m-x+$\frac{1}{2}$>1在(-∞,0)上恒成立;
∴2m>$\frac{1}{2}$+x在(-∞,0)上恒成立;
故2m≥$\frac{1}{2}$,
故m≥-1.
故选:D.
点评 本题考查了函数的性质的应用及恒成立问题与最值问题,属于中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.某公司招聘员工,初试设置计算机、礼仪、专业技能、基本素质共四个科目的考试,要求专业技能、基本素质都要合格,且计算机、礼仪至少有一门合格,则能取得参加复试的资格,现有甲、乙、丙三个人参加初试,每一个人对这四门考试是否合格相互独立,其合格的概率均相同(见表),且每一门课程是否合格相互独立.
(1)求乙取得参加复试的资格的概率;
(2)记ξ表示三个人中取得复试的资格的人数,求ξ的分布及期望Eξ.
| 科目 | 基本素质 | 专业技能 | 计算机 | 礼仪 |
| 合格的概率 | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
(2)记ξ表示三个人中取得复试的资格的人数,求ξ的分布及期望Eξ.
13.已知椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)与直线y=b相交于A、B两点,O是坐标原点,如果△AOB是等边三角形,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{6}$ |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{9}$=1(a>0)的两条渐近线与以椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左焦点为圆心、半径为$\frac{16}{5}$的圆相切,则双曲线的离心率为( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{6}{5}$ |
14.设集合A={x|x2+3x<0},B={x|x<-1},则A∩B=( )
| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|x<-1} | D. | {x|x>0} |
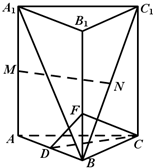 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.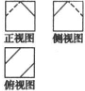 一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.
一个棱长为1的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示,则该几何体的体积为$\frac{23}{24}$.