题目内容
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.
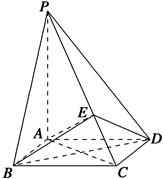
(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.

(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
(1)见解析(2)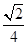 ,
,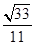
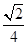 ,
,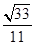
(1)连接AC,因为四边形ABCD是正方形,所以BD⊥AC.因为PA⊥平面ABCD,所以PA⊥BD.
又AC∩PA=A,所以BD⊥平面PAC.
又PC?平面PAC,所以PC⊥BD.
(2)解 ①设PA=x,三棱锥E-BCD的底面积为定值,在△PBC中,易知PB=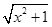 ,PC=
,PC=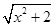 ,
,
又BC=1,故△PBC直角三角形.又BE⊥PC,得EC=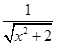 ,可求得该三棱锥的高h=
,可求得该三棱锥的高h=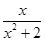 =
=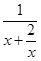 .
.
当且仅当x=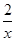 ,即x=
,即x=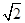 时,三棱锥E-BCD的体积取到最大值,所以h=
时,三棱锥E-BCD的体积取到最大值,所以h=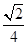 .
.
此时四棱锥E-ABCD的高为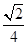 .
.
②以点A为原点,AB,AD,AP所在直线为坐标轴建立空间直角坐标系,则A(0,0,0),C(1,1,0),D(0,1,0),P(0,0,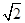 ),易求得CE=
),易求得CE=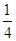 CP.
CP.
所以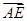 =
=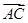 +
+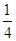
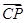 =
=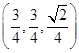 ,
,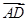 =(0,1,0).
=(0,1,0).
设平面ADE的法向量n1=(x,y,z),则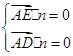
即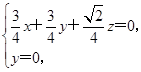 ,令x=
,令x=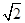 ,则n1=(
,则n1=(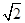 ,0,-3),
,0,-3),
同理可得平面BDE的法向量n2=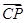 =(-1,-1,
=(-1,-1,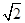 ),所以cos〈n1,n2〉=
),所以cos〈n1,n2〉=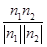 =-
=-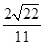 .所以sin〈n1,n2〉=
.所以sin〈n1,n2〉=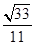 .所以二面角A-DE-B的正弦值的大小为
.所以二面角A-DE-B的正弦值的大小为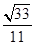 .
.
又AC∩PA=A,所以BD⊥平面PAC.
又PC?平面PAC,所以PC⊥BD.
(2)解 ①设PA=x,三棱锥E-BCD的底面积为定值,在△PBC中,易知PB=
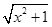 ,PC=
,PC=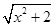 ,
,又BC=1,故△PBC直角三角形.又BE⊥PC,得EC=
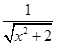 ,可求得该三棱锥的高h=
,可求得该三棱锥的高h=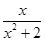 =
=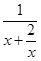 .
.当且仅当x=
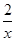 ,即x=
,即x=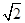 时,三棱锥E-BCD的体积取到最大值,所以h=
时,三棱锥E-BCD的体积取到最大值,所以h=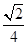 .
.此时四棱锥E-ABCD的高为
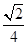 .
.②以点A为原点,AB,AD,AP所在直线为坐标轴建立空间直角坐标系,则A(0,0,0),C(1,1,0),D(0,1,0),P(0,0,
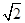 ),易求得CE=
),易求得CE=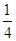 CP.
CP.所以
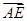 =
=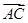 +
+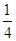
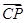 =
=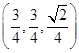 ,
,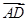 =(0,1,0).
=(0,1,0).设平面ADE的法向量n1=(x,y,z),则
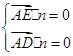
即
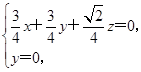 ,令x=
,令x=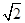 ,则n1=(
,则n1=(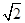 ,0,-3),
,0,-3), 同理可得平面BDE的法向量n2=
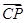 =(-1,-1,
=(-1,-1,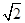 ),所以cos〈n1,n2〉=
),所以cos〈n1,n2〉=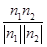 =-
=-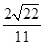 .所以sin〈n1,n2〉=
.所以sin〈n1,n2〉=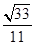 .所以二面角A-DE-B的正弦值的大小为
.所以二面角A-DE-B的正弦值的大小为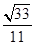 .
.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
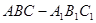 中,四边形
中,四边形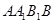 是菱形,四边形
是菱形,四边形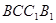 是矩形,
是矩形,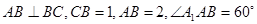 .
.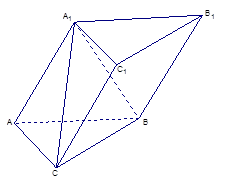
 ;
;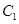 到平面
到平面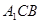 的距离;
的距离;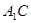 与平面
与平面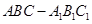 中,点
中,点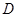 是
是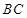 上一点.
上一点.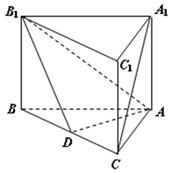
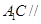 平面
平面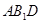 ;
;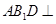 平面
平面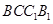 ,求证
,求证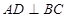 .
.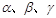 为平面,
为平面,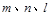 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为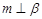 的一个充分条件的是( )
的一个充分条件的是( )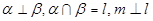
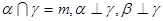
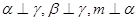
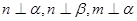
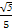
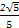

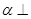 平面
平面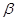 的一个充分条件是
的一个充分条件是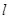 ,
, 且
且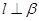
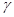 ,
,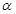 且
且 为两条直线,
为两条直线, 为两个平面,下列四个命题中正确的是
为两个平面,下列四个命题中正确的是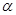 所成的角相等,则
所成的角相等,则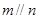
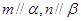 ,
,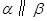 ,则
,则 ,则
,则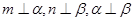 ,则
,则