题目内容
设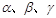 为平面,
为平面,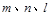 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为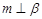 的一个充分条件的是( )
的一个充分条件的是( )
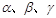 为平面,
为平面,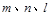 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为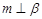 的一个充分条件的是( )
的一个充分条件的是( )A.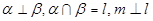 | B.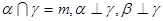 |
C.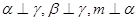 | D.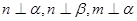 |
D
试题分析:
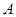 中没有说明
中没有说明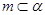 ,直线
,直线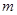 与平面
与平面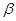 关系不确定,
关系不确定,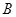 中如果把
中如果把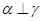 改为
改为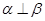 就能得到题设结论,
就能得到题设结论,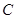 中
中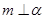 与
与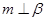 没有任何关系,
没有任何关系, 中由
中由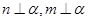 可得
可得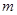 ∥
∥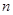 ,再加上
,再加上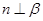 可得
可得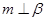 ,选D.
,选D.
练习册系列答案
相关题目
题目内容
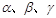 为平面,
为平面,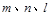 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为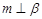 的一个充分条件的是( )
的一个充分条件的是( )A.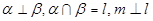 | B.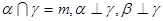 |
C.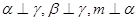 | D.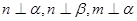 |
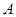 中没有说明
中没有说明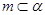 ,直线
,直线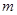 与平面
与平面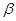 关系不确定,
关系不确定,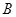 中如果把
中如果把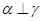 改为
改为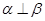 就能得到题设结论,
就能得到题设结论,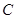 中
中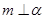 与
与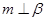 没有任何关系,
没有任何关系, 中由
中由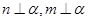 可得
可得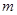 ∥
∥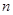 ,再加上
,再加上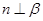 可得
可得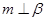 ,选D.
,选D.