题目内容
【题目】已知函数f(x)=sinx-![]() cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+
cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+![]() ))(0<α<
))(0<α<![]() ),且a·b=
),且a·b=![]() .
.
(1)求f(x)在区间![]() 上的最值;
上的最值;
(2)求![]() 的值.
的值.
【答案】(2)最大值是4,最小值是2.(2)![]() .
.
【解析】试题分析:
(1)把函数化为一个角的一个三角函数形式![]() ,再利用正弦函数性质得最值;
,再利用正弦函数性质得最值;
(2)由三角函数周期求出![]() ,再由平面向量数量积的坐标运算公式求出
,再由平面向量数量积的坐标运算公式求出![]() ,化简待求式
,化简待求式![]() 得
得![]() ,最后由同角关系式可得结论.
,最后由同角关系式可得结论.
试题解析:
(1)f(x)=sinx-![]() cosx+2=2sin(x-
cosx+2=2sin(x-![]() )+2,
)+2,
∵x∈[![]() ,
,![]() ],∴x-
],∴x-![]() ∈[
∈[![]() ,π],
,π],
∴f(x)的最大值是4,最小值是2.
(2)∵β=2π,
∴a·b=2+cosαtan(α+π)=2+sinα=![]() ,
,
∴sinα=![]() ,又0<α<
,又0<α<![]() .
.
∴![]() =
=![]() =2cosα=2
=2cosα=2![]() =
=![]() .
.

 期末集结号系列答案
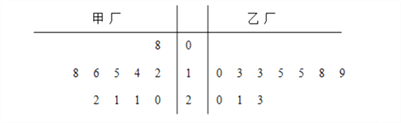
期末集结号系列答案【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为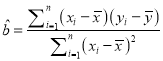 ,
, ![]() )
)
【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
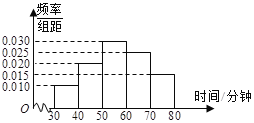
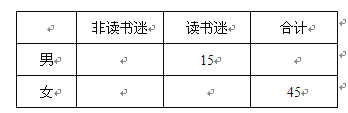
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 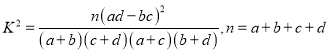
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |