题目内容
【题目】已知函数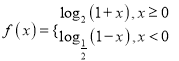 .
.
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)对任意两个实数![]() ,求证:当
,求证:当![]() 时,
时, ![]() ;
;
(3)对任何实数![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 为
为![]() 上的奇函数;(2)证明见解析;(3)
上的奇函数;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)根据函数奇偶性的定义判断函数的奇偶性即可,(2)根据题意有两种情形:①若![]() ,②
,②![]() ,求出
,求出![]() 的表达式,根据函数的性质证明即可;(3)根据函数的单调性问题转化为
的表达式,根据函数的性质证明即可;(3)根据函数的单调性问题转化为![]() ,换元后,根据二次函数的性质求出
,换元后,根据二次函数的性质求出![]() ,即可得
,即可得![]() 的取值范围.
的取值范围.
试题解析:
(1)任取![]() ,则
,则![]() ,
,
![]() ,
,
任取![]() ,则
,则![]() ,
,
![]() ,
,
又![]() ,所以对于任意的
,所以对于任意的![]() ,均有
,均有![]() ,
,
所以函数![]() 为
为![]() 上的奇函数.
上的奇函数.
(2)任取![]() ,当
,当![]() 时,(不妨令
时,(不妨令![]() ),
),
有下列两种情形:(1)若![]() ,
,
则![]() ;
;
(2)若![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() .
.
(3)由(1)(2)得:
对任意两个实数![]() ,当
,当![]() 时,
时, ![]() ,
,
则对任意两个实数![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 为
为![]() 上的单调递增函数,
上的单调递增函数,
![]() 即为
即为![]() ,
,
所以![]() .
.
所以原题意等价于对于任何实数![]() 恒成立,
恒成立,
只需![]() ,而
,而![]() ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.