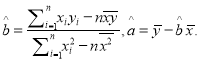题目内容
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为双曲线
,离心率为双曲线![]() 离心率的一半,直线
离心率的一半,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .直线
.直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个相异点,且
两个相异点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在实数![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)设出椭圆的标准方程,利用离心率、四边形的周长进行求解;(Ⅱ)利用平面向量的线性运算得到![]() 的关系,联立直线与椭圆的方程,得到关于
的关系,联立直线与椭圆的方程,得到关于![]() 的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
试题解析:(Ⅰ)根据已知设椭圆![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() ,
,
由已知得![]() ,∴
,∴![]() .
.
∵以椭圆![]() 的长轴和短轴为对角线的四边形的周长为
的长轴和短轴为对角线的四边形的周长为![]() ,
,
∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)根据已知得![]() ,由
,由![]() ,得
,得![]() .
.
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
若![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]() .
.
∴![]() 能使
能使![]() 成立.
成立.
若![]() ,则
,则![]() ,解得
,解得![]() .
.
设![]() ,由
,由![]() 得
得![]() ,
,
由已知得![]() ,即
,即![]() .
.
且![]() .…10分
.…10分
由![]() 得
得![]() ,即
,即![]() .∴
.∴![]() ,
,
∴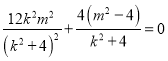 ,即
,即![]() .
.
当![]() 时,
时, ![]() 不成立.∴
不成立.∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上述,当![]() 或
或![]() 或
或![]() 时,
时, ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某项科研活动共进行了5次试验,其数据如下表所示:
特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 555 | 559 | 551 | 563 | 552 |
| 601 | 605 | 597 | 599 | 598 |
(1)从5次特征量![]() 的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(2)求特征量![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并预测当特征量
;并预测当特征量![]() 为570时特征量
为570时特征量![]() 的值.
的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为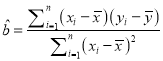 ,
, ![]() )
)