题目内容
设同时满足条件:①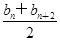 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
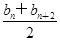 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.(1) 若数列{an}为等差数列,Sn是其前n项和,a3=4,S3=18,求Sn;
(2) 判断(1)中的数列{Sn}是否为“特界” 数列,并说明理由.
(1)-n2+9n(2)是“特界”数列
(1) 设等差数列{an}的公差为d,
则a1+2d=4,3a1+3d=18,解得a1=8,d=-2,Sn=na1+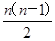 d=-n2+9n.
d=-n2+9n.
(2) 由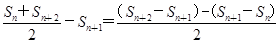
=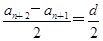 =-1<0,得
=-1<0,得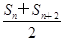 <Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=-
<Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=-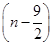 2+
2+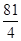 (n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.
(n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.
综上,数列{Sn}是“特界”数列.
则a1+2d=4,3a1+3d=18,解得a1=8,d=-2,Sn=na1+
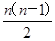 d=-n2+9n.
d=-n2+9n.(2) 由
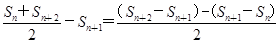
=
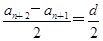 =-1<0,得
=-1<0,得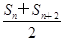 <Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=-
<Sn+1,故数列{Sn}适合条件①,而Sn=-n2+9n=-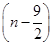 2+
2+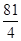 (n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.
(n∈N*),则当n=4或5时,Sn有最大值20.即Sn≤20,故数列{Sn}适合条件②.综上,数列{Sn}是“特界”数列.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 ,an,Sn成等差数列.
,an,Sn成等差数列.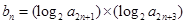 ,求证:
,求证: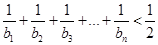 .
.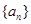 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。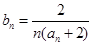 ,求数列
,求数列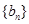 的前
的前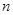 项和
项和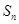
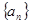
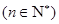 中,其前
中,其前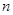 项和为
项和为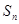 ,满足
,满足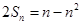 .
.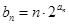 ,求数列
,求数列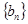 的前
的前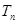 .
.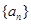 的前
的前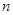 项和为
项和为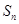 ,且满足
,且满足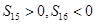 ,则
,则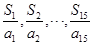 中最大的项为( )
中最大的项为( )


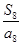
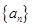 的前n项和
的前n项和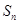 ,若
,若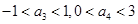 ,则
,则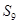 的取值范围是_______.
的取值范围是_______.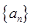 的通项公式an=
的通项公式an=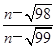 (n∈N*),求数列前30项中的最大项和最小项.
(n∈N*),求数列前30项中的最大项和最小项.