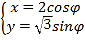题目内容
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() ,直线的参数方程为
,直线的参数方程为![]() ,(
,(![]() 为参数).直线
为参数).直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程.
的普通方程.
(2)设![]() ,若
,若![]() 成等比数列,求
成等比数列,求![]() 和的
和的![]() 值.
值.
【答案】(1)![]() ,
,![]() ;(2)10,
;(2)10,![]() .
.
【解析】
(1)利用直角坐标、极坐标、参数方程互化公式即可解决;
(2)将直线参数方程标准化,联立抛物线方程得到根与系数的关系,再利用直线参数方程的几何意义即可解决.
(1)曲线![]() ,两边同时乘以
,两边同时乘以![]() ,
,
可得![]() ,
,
化简得![]() ;
;
直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() ,
,
可得![]() ,即
,即![]() .
.
(2)直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
化为标准式为 (
(![]() 为参数),代入
为参数),代入![]()
并整理得![]() ,
,
设![]() 两点对应的参数为
两点对应的参数为![]() ,
,
由韦达定理可得![]() ,
,![]() ,
,
由题意得![]() ,即
,即![]() ,
,
可得![]() ,
,
即![]() ,
,![]() ,
,
解得![]() 所以
所以![]() ,
,![]() .
.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
【题目】已知函数![]() .
.
(1)试讨论函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() ,且
,且![]() 恒成立,求a的最大值.
恒成立,求a的最大值.
参考数据:
| 1.6 | 1.7 | 1.74 | 1.8 | 10 |
| 4.953 | 5.474 | 5.697 | 6.050 | 22026 |
| 0.470 | 0.531 | 0.554 | 0.588 | 2.303 |