题目内容
17．已知函数f（x）=2cos2x+sin2x，求函数f（x）的最小值．分析 化简可得（x）=1+$\sqrt{2}$sin（2x+$\frac{π}{4}$），易得最小值．
解答 解：化简可得f（x）=2cos2x+sin2x
=1+cos2x+sin2x=1+$\sqrt{2}$sin（2x+$\frac{π}{4}$），
∴函数f（x）的最小值为：1-$\sqrt{2}$
点评 本题考查三角函数的最值，涉及三角函数恒等变换，属基础题．
练习册系列答案
相关题目
8．在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x其中x∈（0，1），以A，B为焦点且过点D的双曲线的离心率为e1，以C，D为焦点且过点A的椭圆的离心率为e2，若对任意x∈（0，1）不等式t＜e1+e2恒成立，则t的最大值为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | 2 | D． | $\sqrt{2}$ |
12．已知集合A={x|3x-x2＞0}，B={0，1，2，3}，则A∩B等于（ ）
| A． | {0，1} | B． | {1，2} | C． | {1，2，3} | D． | {0，1，2，3} |
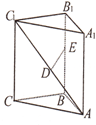如图，直三棱柱ABC一A1B1C1中，AB=$\sqrt{2}$，AC=3，BC=$\sqrt{5}$，D是ACl的中点，E是侧棱BB1上的一个动点