题目内容
9.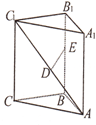 如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点
如图,直三棱柱ABC一A1B1C1中,AB=$\sqrt{2}$,AC=3,BC=$\sqrt{5}$,D是ACl的中点,E是侧棱BB1上的一个动点(1)当E是BB1的中点时,证明:DE∥平面A1B1C1
(2)在棱BB1上是否存在点E使平面AC1E⊥平面AC1C?若存在,求出$\frac{BE}{{B{B_1}}}$的值,若不存在,说明理由.
分析 (1)如图,取A1C1中点M,连B1M,MD,可证MD$\stackrel{∥}{=}$B1E,既有四边形MDEB为平行四边形,可证MB1∥DE,又DE?平面A1B1C1,MB1?平面A1B1C1,即可证明DE∥平面A1B1C1.
(2)过B1作B1Q⊥A1C1于Q,既有B1Q⊥平面CAC1,假设满足题意的点E存在,则过E作EP⊥AC1于P,可证EP$\stackrel{∥}{=}$B1Q,设BB1=x,BE=y,可得$\frac{PQ}{A{A}_{1}}=\frac{{C}_{1}Q}{{C}_{1}{A}_{1}}$,在△A1B1C1中,由余弦定理可求cos∠B1C1A1,从而可得sin∠B1C1A1,由三角形面积公式可求B1Q,C1Q,从而可求出$\frac{BE}{{B{B_1}}}$的值.
解答  证明:(1)如图,取A1C1中点M,连B1M,MD,
证明:(1)如图,取A1C1中点M,连B1M,MD,
在△C1A1A中,DM$\stackrel{∥}{=}$$\frac{1}{2}$AA1=$\frac{1}{2}$BB1,…2分
∴MD$\stackrel{∥}{=}$B1E,∴四边形MDEB为平行四边形,
∴MB1∥DE,又DE?平面A1B1C1,MB1?平面A1B1C1,
∴DE∥平面A1B1C1…5分
(2)过B1作B1Q⊥A1C1于Q,∵直三棱柱ABC-A1B1C1,
∴B1Q⊥平面CAC1,
假设满足题意的点E存在,则过E作EP⊥AC1于P,由于平面AC1E⊥平面AC1C,则EP⊥PC,
又BB1∥平面CAC1,∴EP$\stackrel{∥}{=}$B1Q,
设BB1=x,BE=y,
∴PQ$\stackrel{∥}{=}$B1E,$\frac{PQ}{A{A}_{1}}=\frac{{C}_{1}Q}{{C}_{1}{A}_{1}}$…9分
在△A1B1C1中,由余弦定理cos∠B1C1A1=$\frac{5+9-2}{6\sqrt{5}}$=$\frac{2}{\sqrt{5}}$,
∴sin∠B1C1A1=$\sqrt{1-\frac{4}{5}}$=$\frac{\sqrt{5}}{5}$,
由${S}_{{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}×\sqrt{5}×3×\frac{\sqrt{5}}{5}$=$\frac{1}{2}×3×{B}_{1}Q$可得B1Q=1…10分
在Rt△C1QB1中,C1Q=$\sqrt{5-1}$=2,
∴$\frac{PQ}{A{A}_{1}}=\frac{{C}_{1}Q}{{C}_{1}{A}_{1}}=\frac{2}{3}=\frac{E{B}_{1}}{B{B}_{1}}$,
∴$\frac{BE}{B{B}_{1}}$=$\frac{B{B}_{1}-E{B}_{1}}{B{B}_{1}}$=1-$\frac{2}{3}=\frac{1}{3}$,
即:存在满足题意的点E,此时有$\frac{BE}{B{B}_{1}}=\frac{1}{3}$…12分
点评 本题主要考查了平面与平面垂直的性质,直线与平面平行的判定,考查了空间想象能力和推理论证能力及转化思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案 已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°
已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°