题目内容
10.己知函数f(x)满足f(1)=$\frac{1}{4}$,对任意x,y∈R都有4f(x)f(y)=f(x+y)+f(x-y),则f(2017)=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
分析 根据条件判断函数f(x)是周期函数,利用函数的周期性进行求解即可.
解答 解:取x=1,y=0得$f(0)=\frac{1}{2}$
法一:根据已知知$f(1)=\frac{1}{4}$
取x=1,y=1得f(2)=-$\frac{1}{4}$
取x=2,y=1得f(3)=-$\frac{1}{2}$
取x=2,y=2得f(4)=-$\frac{1}{4}$
取x=3,y=2得f(5)=$\frac{1}{4}$
取x=3,y=3得f(6)=$\frac{1}{2}$
猜想得周期为6;
法二:取x=1,y=0得$f(0)=\frac{1}{2}$
取x=n,y=1,有f(n)=f(n+1)+f(n-1),
同理f(n+1)=f(n+2)+f(n)
联立得f(n+2)=-f(n-1)
所以f(n)=-f(n+3)=f(n+6)
所以函数是周期函数,周期T=6,
故f(2017)=f(336×6+1)=f(1)=$\frac{1}{4}$,
故选:A.
点评 本题主要考查函数值的计算,准确找出周期是此类问题(项数很大)的关键,分别可以用归纳法和演绎法得出周期,解题时根据自己熟悉的方法得出即可.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
20.函数$f(x)=-\frac{1}{1+x}$在x∈[1,+∞)上的值域为( )
| A. | $({-∞,-\frac{1}{2}}]$ | B. | $[{-\frac{1}{2},+∞})$ | C. | $[{-\frac{1}{2},0})$ | D. | $[-\frac{1}{2},0]$ |
18.若将函数f(x)=2sin(3x+$\frac{5π}{12}$)的图象向右平移$\frac{2π}{9}$个单位后得到函数g(x)的图象,g($\frac{1}{3}$x)在[-$\frac{π}{3}$,$\frac{5π}{6}$]上的最大值( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
5.若关于x的方程ax2+bx+c=0(a≠0)的两个实根为1或2,则函数f(x)=cx2+bx+a的零点为( )
| A. | 1,2 | B. | -1,-2 | C. | 1,$\frac{1}{2}$ | D. | -1,-$\frac{1}{2}$ |
15.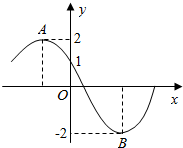 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -2 |
20.函数f(x)=$|tan(2x-\frac{π}{4})|$的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | π | D. | $\frac{π}{2}$ |
 已知函数y=f(x)是奇函数,根据y=f(x)在[0,5]上的图象作出y=f(x)在[-5,0)上的图象.
已知函数y=f(x)是奇函数,根据y=f(x)在[0,5]上的图象作出y=f(x)在[-5,0)上的图象.