题目内容
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB="90° "
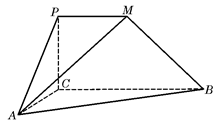
(1)求证:AC⊥BM;
(2)求二面角M-AB-C的余弦值
(3求P到平面MAB的距离

(1)求证:AC⊥BM;
(2)求二面角M-AB-C的余弦值
(3求P到平面MAB的距离
(1)证明略
(2)
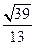
(4)
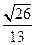
 面
面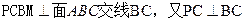
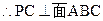 ┅┅┅┅2分
┅┅┅┅2分如图以
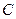 为原点建立空间直角坐标系
为原点建立空间直角坐标系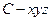 .
. 设

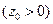 ,有
,有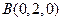 ,
,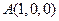 ,
, 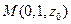 .
. 
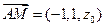 ,
,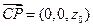
由直线
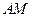 与直线
与直线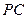 所成的角为60°,得
所成的角为60°,得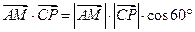
即
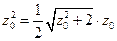 ,解得
,解得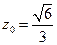 .┅┅┅5分
.┅┅┅5分(1)∴
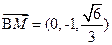 ,
,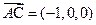 ,
,得
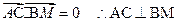 ┅┅┅6分
┅┅┅6分∴
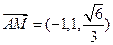 ,
,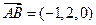
(2)设平面
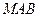 的一个法向量为
的一个法向量为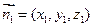 ,则
,则由
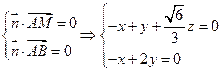 ,取
,取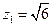 ,得
,得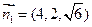 ┅┅┅┅8分
┅┅┅┅8分取平面
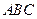 的一个法向量为
的一个法向量为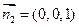
则
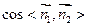
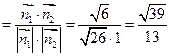 ┅┅┅┅10分
┅┅┅┅10分由图知二面角
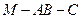 的大小的余弦值为
的大小的余弦值为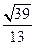 ┅┅┅┅11分
┅┅┅┅11分(3)
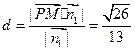 故P到平面MAB的距离为
故P到平面MAB的距离为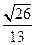 ┅┅┅┅13分
┅┅┅┅13分
练习册系列答案
相关题目
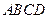 为矩形,
为矩形,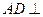
 平面ABE
平面ABE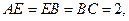
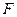 为
为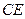 上的点,且
上的点,且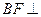 平
平 面
面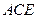 ,
,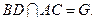
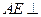 平面
平面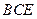 ;
;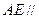 平面
平面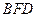 ;
;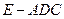 的体积.
的体积. 中,
中, 是棱
是棱 的中点,
的中点, 为平面
为平面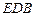 内一点,
内一点,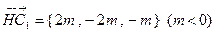 .
.
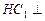 平面
平面 与平面
与平面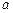 ,求三棱锥
,求三棱锥 的体积.
的体积.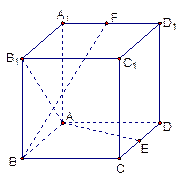
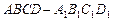 中,E,F分别是CD,A1D1中点
中,E,F分别是CD,A1D1中点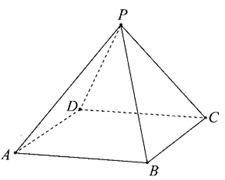
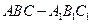 中,侧面
中,侧面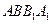 ,
,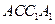 均为正方形,∠
均为正方形,∠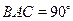 ,点
,点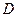 是棱
是棱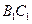 的中点.
的中点.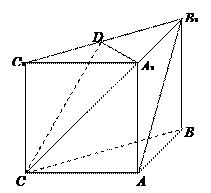
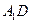 ⊥平面
⊥平面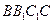 ;
;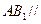 平面
平面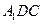 ;
;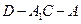 的余弦值
的余弦值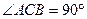 ,E、F分别是BA、BC的中点,G是AA1上一点,且
,E、F分别是BA、BC的中点,G是AA1上一点,且

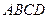 和矩形
和矩形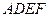 所在平面相互垂直,
所在平面相互垂直,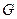 是
是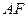 的中点.
的中点.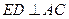 ;
; 与平面
与平面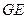 与
与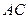 所成角的余弦值.
所成角的余弦值.