题目内容
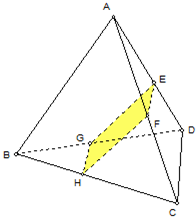
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2.
(Ⅰ)求异面直线EF与BC所成角的大小;
(Ⅱ)若二面角A-BF-D的平面角的余弦值为
,求AB的长.
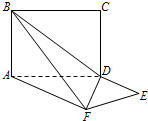
(Ⅰ)求异面直线EF与BC所成角的大小;
(Ⅱ)若二面角A-BF-D的平面角的余弦值为
| 1 |
| 3 |

(Ⅰ)延长AD,FE交于Q.
∵ABCD是矩形,
∴BC∥AD,
∴∠AQF是异面直线EF与BC所成的角.
在梯形ADEF中,由DE∥AF,AF⊥FE,AF=2,DE=1得
∠AQF=30°.
即异面直线EF与BC所成角为30°…(7分)
(Ⅱ)方法一:
设AB=x.取AF的中点G.由题意得
DG⊥AF.
∵平面ABCD⊥平面ADEF,AB⊥AD,
∴AB⊥平面ADEF,
∴AB⊥DG.
∴DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连接DH,则DH⊥BF,
∴∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得
DG=
.
在直角△BAF中,由
=sin∠AFB=
,得
=
,
∴GH=
.
在直角△DGH中,DG=
,GH=
,得
DH=2
.
∵cos∠DHG=
=
,得x=
,
∴AB=
.…(15分)
方法二:设AB=x.
以F为原点,AF,FQ所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.则
F(0,0,0),A(-2,0,0),E(0,
,0),D(-1,
,0),B(-2,0,x),
∴
=(1,-
,0),
=(2,0,-x).
∵EF⊥平面ABF,所以平面ABF的法向量可取
=(0,1,0).
设
=(x1,y1,z1)为平面BFD的法向量,则
∴可取
=(
,1,
).
∵cos<
,
>=
=
,得x=
,
∴AB=
.
…(15分)

∵ABCD是矩形,
∴BC∥AD,
∴∠AQF是异面直线EF与BC所成的角.
在梯形ADEF中,由DE∥AF,AF⊥FE,AF=2,DE=1得
∠AQF=30°.
即异面直线EF与BC所成角为30°…(7分)
(Ⅱ)方法一:
设AB=x.取AF的中点G.由题意得
DG⊥AF.
∵平面ABCD⊥平面ADEF,AB⊥AD,
∴AB⊥平面ADEF,
∴AB⊥DG.
∴DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连接DH,则DH⊥BF,
∴∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得
DG=
| 3 |
在直角△BAF中,由
| AB |
| BF |
| GH |
| FG |
| GH |
| x |
| 1 | ||
|
∴GH=
| x | ||
|
在直角△DGH中,DG=
| 3 |
| x | ||
|
DH=2
|
∵cos∠DHG=
| GH |
| DH |
| 1 |
| 3 |
| 2 |
| 5 |
| 15 |
∴AB=
| 2 |
| 5 |
| 15 |

方法二:设AB=x.
以F为原点,AF,FQ所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.则
F(0,0,0),A(-2,0,0),E(0,
| 3 |
| 3 |
∴
| DF |
| 3 |
| BF |
∵EF⊥平面ABF,所以平面ABF的法向量可取
| n1 |
设
| n2 |
|
∴可取
| n2 |
| 3 |
2
| ||
| x |
∵cos<
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 3 |
| 2 |
| 5 |
| 15 |
∴AB=
| 2 |
| 5 |
| 15 |
…(15分)


练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分别交
分别交 于点
于点 ,将该正方形沿
,将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱 中
中
 ;
; 上有一点
上有一点 ,
, ,
, 面
面
 与平面
与平面