题目内容
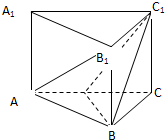
正方体ABCD-A1B1C1D1棱长为2，E是棱A1B1的中点．
（1）求异面直线A1B1与BD的距离；
（2）求直线EC1与BD所成角的大小．
（1）求异面直线A1B1与BD的距离；
（2）求直线EC1与BD所成角的大小．
（1）∵B1B⊥AB，B1B⊥BC，
∴B1B⊥平面ABCD
∴B1B⊥BD
又B1B⊥A1B1，
∴线段B1B的长即为所求．
∵B1B=2，
∴异面直线A1B1与BD的距离为2．
（2）取A1D1中点H
∴EH∥B1D1
∴EH∥BD
∴EC1与BD所成角为∠HEC1（或其补角）
设正方体棱长为2，则HE=
，EC1=
，HC1=
∴cos∠HEC1=
=
=
＞0
∴EC1与BD所成角为arccos
∴B1B⊥平面ABCD
∴B1B⊥BD
又B1B⊥A1B1，
∴线段B1B的长即为所求．
∵B1B=2，
∴异面直线A1B1与BD的距离为2．
（2）取A1D1中点H
∴EH∥B1D1
∴EH∥BD
∴EC1与BD所成角为∠HEC1（或其补角）
设正方体棱长为2，则HE=
| 2 |
| 5 |
| 5 |
∴cos∠HEC1=
| HE2+EC12-HC12 |
| 2HE×EC1 |
| 2+5-5 | ||||
2×
|
| ||
| 10 |
∴EC1与BD所成角为arccos
| ||
| 10 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
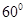，则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________．
