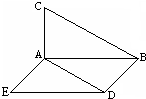
题目内容
三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,点E、F分别在AC,AD上,使平面BEF⊥平面ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为 ( )
A. | B. | C. | D. |
B.
∵CD⊥平面ABC,∴平面ABC⊥平面ACD,又∵平面
BEF⊥平面ACD,且平面ABC 平面BEF=BE,∴BE⊥平
平面BEF=BE,∴BE⊥平
面ACD,∴BE⊥AC,作BM∥CD,易知∠EBC为所求平
面角.在Rt△ABC中可得 .
.
BEF⊥平面ACD,且平面ABC
 平面BEF=BE,∴BE⊥平
平面BEF=BE,∴BE⊥平面ACD,∴BE⊥AC,作BM∥CD,易知∠EBC为所求平
面角.在Rt△ABC中可得
 .
.
练习册系列答案
相关题目

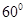 ,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.
,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________.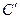 ,若直角边AB=
,若直角边AB=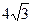 ,AC=
,AC=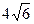 ,则二面角A-B
,则二面角A-B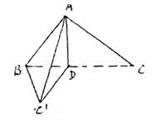



 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分别交
分别交 于点
于点 ,将该正方形沿
,将该正方形沿 折叠,使得
折叠,使得 与
与 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱 中
中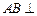
 ;
; 上有一点
上有一点 ,
, ,
, 面
面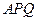
 与平面
与平面