题目内容
(本小题满分13分)
若数列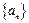 满足
满足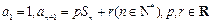 ,
,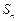 为数列
为数列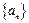 的前
的前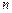 项和.
项和.
(Ⅰ) 当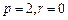 时,求
时,求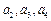 的值;
的值;
(Ⅱ)是否存在实数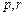 ,使得数列
,使得数列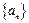 为等比数列?若存在,求出
为等比数列?若存在,求出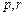 满足的条件;若不存在,说明理由.
满足的条件;若不存在,说明理由.
若数列
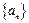 满足
满足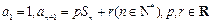 ,
,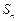 为数列
为数列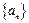 的前
的前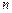 项和.
项和.(Ⅰ) 当
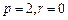 时,求
时,求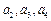 的值;
的值;(Ⅱ)是否存在实数
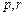 ,使得数列
,使得数列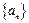 为等比数列?若存在,求出
为等比数列?若存在,求出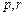 满足的条件;若不存在,说明理由.
满足的条件;若不存在,说明理由.(1)18;(2)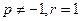
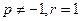
(I)因为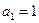 ,
,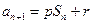 ,
,
当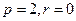 时,
时,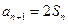 …………… 1分
…………… 1分
所以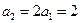 , …………… 2分
, …………… 2分
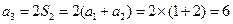 , ……………4分
, ……………4分
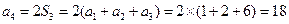 . ……………6分
. ……………6分
(II)因为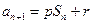 ,
,
所以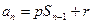 (
(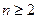 ), ……………7分
), ……………7分
所以 ,
,
即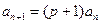 ,其中
,其中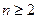 , ……………9分
, ……………9分
所以若数列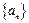 为等比数列,则公比
为等比数列,则公比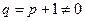 ,所以
,所以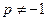 , ……………11分
, ……………11分
又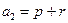 =
=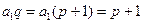 ,故
,故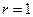 . ……………13分
. ……………13分
所以当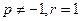 时,数列
时,数列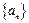 为等比数列
为等比数列
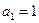 ,
,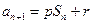 ,
,当
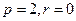 时,
时,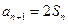 …………… 1分
…………… 1分所以
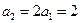 , …………… 2分
, …………… 2分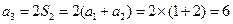 , ……………4分
, ……………4分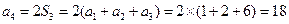 . ……………6分
. ……………6分(II)因为
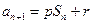 ,
,所以
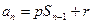 (
(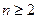 ), ……………7分
), ……………7分所以
 ,
, 即
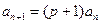 ,其中
,其中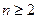 , ……………9分
, ……………9分所以若数列
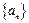 为等比数列,则公比
为等比数列,则公比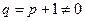 ,所以
,所以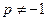 , ……………11分
, ……………11分又
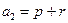 =
=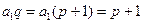 ,故
,故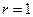 . ……………13分
. ……………13分所以当
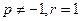 时,数列
时,数列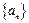 为等比数列
为等比数列
练习册系列答案
相关题目
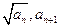 )(n
)(n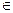 N*)在函数y=x2+1的图象上
N*)在函数y=x2+1的图象上 (Ⅰ)求数列{an}的通项公式;(Ⅱ)若数列{bn}满足bn=
(Ⅰ)求数列{an}的通项公式;(Ⅱ)若数列{bn}满足bn=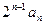 (n∈N*),求数列{bn}的前n项和
(n∈N*),求数列{bn}的前n项和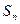 。
。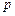 ,
,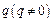 是实数,方程
是实数,方程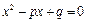 有两个实根
有两个实根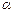 ,
,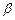 ,数列
,数列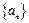 满足
满足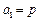 ,
,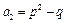 ,
,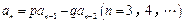
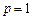 ,
,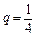 ,求
,求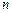 项和.
项和.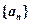 、
、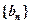 的前n项和分别为
的前n项和分别为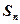 、
、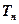 ,
,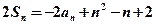 ,
,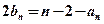 .
.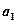 、
、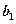 的值,并证明数列
的值,并证明数列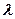 的值,使数列
的值,使数列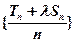 是等差数列.
是等差数列.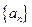 的前n项和为
的前n项和为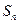 ,若对任意的r、s
,若对任意的r、s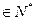 ,都有
,都有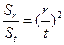 .
.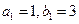 ,数列
,数列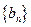 的第n项是数列
的第n项是数列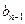 项
项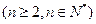 ,求
,求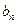 ;
;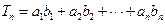 .
.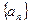 中,若
中,若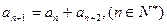 ,则称数列
,则称数列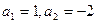 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;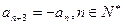 ;
;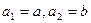 ,若数列
,若数列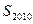 。
。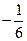 的等差数列,如果
的等差数列,如果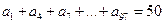 ,那么
,那么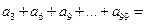 ( )
( )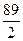
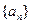 的递推公式
的递推公式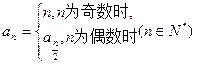 求出这个数列各项的值,使得这个数列中的每一项都是奇数。则
求出这个数列各项的值,使得这个数列中的每一项都是奇数。则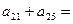 ;
;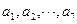 中,恰好有5个
中,恰好有5个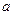 ,2个
,2个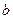
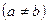 ,则不相同的数列共有 个.
,则不相同的数列共有 个.