题目内容
我们可以利用数列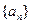
的递推公式
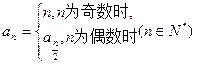求出这个数列各项的值，使得这个数列中的每一项都是奇数。则
；
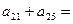研究发现，该数列中的奇数都会重复出现，那么第8个5是该数列的第 项。
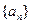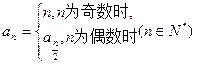的递推公式求出这个数列各项的值，使得这个数列中的每一项都是奇数。则 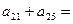；研究发现，该数列中的奇数都会重复出现，那么第8个5是该数列的第 项。
28，640
略
练习册系列答案
相关题目
题目内容
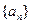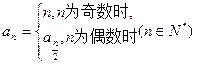的递推公式求出这个数列各项的值，使得这个数列中的每一项都是奇数。则 ；
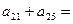的前n项和为
，
，
,等差数列
中
，且
，又
、
、
成等比数列.
的前n项和
. 
的公比
，
是
和
的一个等比中项，
和
的等差中项为
，若数列
满足
（
）．
的前
项和
．
满足
，
为数列
项和.
时，求
的值；
，使得数列
的前
项和为
，若对任意的
，
，都有
．
的第
是数列
项
，且
，
，求数列
．
是等差数列，且公差为
，若数列
中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”.
，求证：该数列是“封闭数列”；
是否是“封闭数列”，为什么？
是数列
项和，若公差
，试问：是否存在这样的“封闭数列”，使
；若存在，求
的各项为正，且
，则
．
中，
，
，则
（ ）
