题目内容
7.现有下列命题,其中正确的命题的序号为( )①命题“?x∈R,x2+x+1=0”的否定是“?x∈R,x2+x+1≠0”;
②若A={x|x>0},B={x|x≤-1},则A∩(∁RB)=A;
③直线(m+2)x+3my+1=0与(m-2)x+(m+2)y-3=0互相垂直的条件为m=-2;
④如果抛物线y=ax2的准线方程为y=1,则a=-$\frac{1}{4}$.
| A. | ②④ | B. | ①② | C. | ③④ | D. | ②③ |
分析 利用命题的否定判断①的正误;利用交并补的运算判断②的正误;利用垂直的充要条件判断③的正误;通过抛物线的准线方程判断④的正误;
解答 解:对于①命题的否定为:“?x∈R,x2+x+1≠0”;所以①不正确;
对于②A∩(∁RB)={x|x>0}=A;所以②正确;
对于③由(m+2)(m-2)-3m(m+2)=0,得m=-2或$\frac{1}{2}$;所以③不正确;
对于④抛物线的标准方程为x2=-2($\frac{1}{-2a}$)y,由准线方程为:y=1,可得$-\frac{1}{4a}=1$,
即a=-$\frac{1}{4}$.所以④正确;
故选A.
点评 本题考查命题的真假的判断与应用,命题的否定、交并补的运算,直线的垂直条件以及抛物线的性质,考查基本知识的应用.

练习册系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}3,x≥m\\{x}^{2}+5x-12,x<m\end{array}\right.$,若函数g(x)=f(x)-x恰有三个不同的零点,则实数m的取值范围是( )
| A. | m<2 | B. | 2<m≤3 | C. | 2≤m≤3 | D. | m>3 |
15.已知a,b是实数,则“a>|b|”是“a2>b2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
16.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,则该数列的前11项和为( )
| A. | 12 | B. | 72 | C. | 132 | D. | 192 |
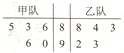 某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:
某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示: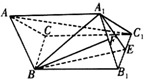 如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.
如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°. (1)求⊙P的半径(用θ表示);
(1)求⊙P的半径(用θ表示);