题目内容
2.抛掷三枚不同的具有正、反两面的金属制品A1、A2、A3,假定A1正面向上的概率为$\frac{1}{2}$,A2正面向上的概率为$\frac{1}{3}$,A3正面向上的概率为t(0<t<1),把这三枚金属制品各抛掷一次,设ξ表示正面向上的枚数.(1)求ξ的分布列及数学期望Eξ(用t表示);
(2)令an=(2n-1)cos($\frac{6nπ}{5+6t}$Eξ)(n∈N+),求数列{an}的前n项和.
分析 (1)通过求出ξ=0、1、2、3时相应的概率,进而求出ξ的分布列及数学期望Eξ;
(2)通过(1)、化简可知an=(-1)n(2n-1),进而分n为奇数、偶数两种情况讨论即可求出Sn.
解答 解:(1)依题意,ξ的可能取值为0、1、2、3,
P(ξ=0)=$\frac{1}{2}$•$\frac{2}{3}$•(1-t)=$\frac{2-2t}{6}$,
P(ξ=1)=$\frac{1}{2}$•$\frac{2}{3}$•(1-t)+$\frac{1}{2}$•$\frac{1}{3}$•(1-t)+$\frac{1}{2}$•$\frac{2}{3}$•t=$\frac{3-t}{6}$,
P(ξ=2)=$\frac{1}{2}$•$\frac{1}{3}$•(1-t)+$\frac{1}{2}$•$\frac{2}{3}$•t+$\frac{1}{2}$•$\frac{1}{3}$•t=$\frac{2t+1}{6}$,
P(ξ=3)=$\frac{1}{2}$•$\frac{1}{3}$•t=$\frac{t}{6}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{2-2t}{6}$ | $\frac{3-t}{6}$ | $\frac{2t+1}{6}$ | $\frac{t}{6}$ |
(2)由(1)可知an=(2n-1)cos($\frac{6nπ}{5+6t}$•$\frac{5+6t}{6}$)
=(2n-1)cos(nπ)
=(-1)n(2n-1),
当n为偶数时,Sn=[(-1)+3]+[(-5)+7]+…+[-(2n-3)+(2n-1)]
=2•$\frac{n}{2}$
=n;
当n为奇数时,Sn=[(-1)+3]+[(-5)+7]+…+[-(2n-5)+(2n-3)]+[-(2n-1)]
=2•$\frac{n-1}{2}$-(2n-1)
=n-1-2n+1
=-n;
综上所述,Sn=(-1)n•n.
点评 本题考查离散型随机变量及其分布列、期望,考查数列的求和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.如图,在△OAB中,P为线段AB上的一点,若$\overrightarrow{{O}{P}}$=x$\overrightarrow{{O}{A}}$+y$\overrightarrow{{O}{B}}$,且$\overrightarrow{{B}{P}}$=2$\overrightarrow{{P}{A}}$,则$\frac{x}{y}$等于( )

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
13.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{x+y≤1}\\{y≤mx+m}\end{array}\right.$下,目标函数z=x+5y的最小值为-8,则m的值为( )
| A. | 3 | B. | $\frac{13}{5}$ | C. | 4 | D. | 8 |
7.复数z满足(z+2)(1+i3)=2(i为虚数单位),则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
14.函数y=$\frac{x}{x+1}$的图象是( )
| A. |  | B. |  | C. |  | D. | 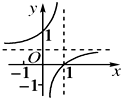 |
12.“m≤2”是“方程x3-3x+m=0”在[0,2]上有解的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |