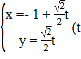题目内容
【题目】设函数![]() .
.
![]() 求函数
求函数![]() 的单调区间和极值.
的单调区间和极值.
![]() 若函数
若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围.
内恰有两个零点,求a的取值范围.
【答案】(1)见解析; (2)![]()
【解析】
![]() 求出函数的导数,通过讨论a的范围,求出函数的单调区间和极值即可;
求出函数的导数,通过讨论a的范围,求出函数的单调区间和极值即可;
![]() 通过讨论a的范围,若满足
通过讨论a的范围,若满足![]() 在区间
在区间![]() 内恰有两个零点,需满足
内恰有两个零点,需满足 ,解出即可.
,解出即可.
![]() 由
由![]() ,得
,得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,函数无极大值,也无极小值;
上单调递增,函数无极大值,也无极小值;
![]() 当
当![]() 时,由
时,由![]() ,得
,得![]() 或
或![]() 舍去
舍去![]() .
.
于是,当x变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
x |
|
|
|
|
| 0 |
|
| 递减 |
| 递增 |
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
综上可知,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,函数既无极大值也无极小值;
,函数既无极大值也无极小值;
当![]() 时,函数
时,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间为
,单调递增区间为![]() ,
,
函数![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
![]() 当
当![]() 时,由
时,由![]() 知函数
知函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故函数![]() 在区间
在区间![]() 上至多有一个零点,不合题意.
上至多有一个零点,不合题意.
当![]() 时,由
时,由![]() 知,当
知,当![]() 时,函数
时,函数![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 单调递增,
单调递增,
所以函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
若函数![]() 在区间
在区间![]() 内恰有两个零点,
内恰有两个零点,
则需满足 ,即
,即 整理得
整理得 ,所以
,所以![]() .
.
故所求a的取值范围为![]()

 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】2018年11月5日上午,首届中国国际进口博览会拉开大幕,这是中国也是世界上首次以进口为主题的国家级博览会,本次博览会包括企业产品展、国家贸易投资展,其中企业产品展分为7个展区,每个展区统计了备受关注百分比,如下表:
展区类型 | 智能及高端装备 | 消费电子及家电 | 汽车 | 服装服饰及日用消费品 | 食品及农产品 | 医疗器械及医药保健 | 服务贸易 |
展区的企业数 | 400 | 60 | 70 | 650 | 1670 | 300 | 450 |
备受关注百分比 |
|
|
|
|
|
|
|
备受关注百分比指:一个展区中受到所有相关人士关注![]() 简称备受关注
简称备受关注![]() 的企业数与该展区的企业数的比值.
的企业数与该展区的企业数的比值.
(1)从企业产品展7个展区的企业中随机选取1家,求这家企业是选自“智能及高端装备”展区备受关注的企业的概率;
(2)某电视台采用分层抽样的方法,在“消费电子及家电”展区备受关注的企业和“医疗器械及医药保健”展区备受关注的企业中抽取6家进行了采访,若从受访企业中随机抽取2家进行产品展示,求恰有1家来自于“医疗器械及医药保健”展区的概率.