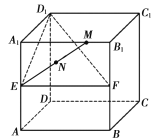
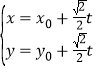题目内容
【题目】设函数![]() .① 若
.① 若![]() ,则
,则![]() 的极小值为___; ② 若存在
的极小值为___; ② 若存在![]() 使得方程
使得方程![]() 无实根,则
无实根,则![]() 的取值范围是___.
的取值范围是___.
【答案】![]()
![]()
【解析】
①判断函数的单调性,结合函数极值的定义进行判断即可
②根据分段函数的表达式求出函数f(x)的取值范围,若方程无实根,等价为f(x)与y=m没有交点,利用函数与方程的关系进行转化求解即可.
①当a=0时,当x≤0时,f(x)=x为增函数,
当x>0时,f(x)=x2﹣2x﹣4,对称轴为x=1,
当0<x≤1时,f(x)为减函数,当x≥1时,f(x)为增函数,
即当x=1时,函数取得极小值,此时f(1)=1﹣2﹣4=﹣5,
②∵当x≤a时,f(x)≤a,
当x→+∞时,f(x)→+∞,
若存在m使得方程f(x)﹣m=0无实根,即存在m使得方程f(x)=m无实根,
则说明函数f(x)的值域不是R,
即当x>a时,f(x)>a,即可.
若a<1,当x>a时,f(x)的最小值为f(1)=1﹣2﹣4=﹣5,
此时只要a<﹣5即可,
若a≥1,此时f(x)在(a,+∞)为增函数,则f(x)>f(a)=a2﹣2a﹣4,
由a2﹣2a﹣4>a,即a2﹣3a﹣4>0,得(a+1)(a﹣4)>0,
则a>4或a<﹣1(舍),
综上a>4或a<﹣5,
即实数a的取值范围是(﹣∞,﹣5)∪(4,+∞),
故答案为:﹣5,(﹣∞,﹣5)∪(4,+∞).

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目