题目内容
如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1＝AB＝2，BC＝3.
(1)求证：AB1∥平面BC1D；
(2)求四棱锥B－AA1C1D的体积．
（1）见解析（2）3
【解析】(1)证明：如图，连接B1C，设B1C与BC1相交于点O，连接OD，
∵四边形BCC1B1是平行四边形，
∴点O为B1C的中点．
∵D为AC的中点，∴OD为△AB1C的中位线，
∴OD∥AB1，
∵OD?平面BC1D，AB1?平面BC1D，∴AB1∥平面BC1D.
(2)∵AA1⊥平面ABC，AA1?平面AA1C1C，
∴平面ABC⊥平面AA1C1C，
作BE⊥AC，垂足为E，则BE⊥平面AA1C1C.
在Rt△ABC中，AC＝
，BE＝
＝
，
∴四棱锥B－AA1C1D的体积V＝
×
(A1C1＋AD)·AA1·BE＝
×
×2×
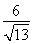＝3.
练习册系列答案
相关题目
