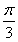题目内容
已知两直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0.求分别满足下列条件的a，b的值．
(1)直线l1过点(－3，－1)，并且直线l1与l2垂直；
(2)直线l1与直线l2平行，并且坐标原点到l1，l2的距离相等．
（1）a＝2，b＝2.（2）a＝2，b＝－2或a＝
，b＝2
【解析】(1)∵l1⊥l2，∴a(a－1)＋(－b)·1＝0，即a2－a－b＝0. ①
又点(－3，－1)在l1上，∴－3a＋b＋4＝0. ②
由①②得，a＝2，b＝2.
(2)∵l1∥l2，∴
＝1－a，∴b＝
，故l1和l2的方程可分别表示为
(a－1)x＋y＋
＝0，(a－1)x＋y＋
＝0，
又原点到l1与l2的距离相等，∴4 
＝
，
∴a＝2或a＝
，∴a＝2，b＝－2或a＝，b＝2.
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
