题目内容
已知函数 ,
, .
.
(Ⅰ)已知 ,若
,若 ,求
,求 的值;
的值;
(Ⅱ)设 ,当
,当 时,求
时,求 在
在 上的最小值;
上的最小值;
(Ⅲ)求函数 在区间
在区间 上的最大值.
上的最大值.
 ,
, .
.(Ⅰ)已知
 ,若
,若 ,求
,求 的值;
的值;(Ⅱ)设
 ,当
,当 时,求
时,求 在
在 上的最小值;
上的最小值;(Ⅲ)求函数
 在区间
在区间 上的最大值.
上的最大值.(Ⅰ)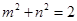 ;(Ⅱ)当
;(Ⅱ)当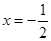 时,
时, 最小值为
最小值为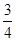 ;(Ⅲ)当
;(Ⅲ)当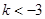 时,
时,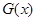 在
在 上的最大值为0;当
上的最大值为0;当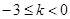 时,
时,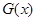 在
在 上的最大值为
上的最大值为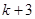 ;当
;当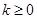 时,
时,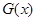 在
在 上的最大值为
上的最大值为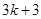 .
.
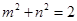 ;(Ⅱ)当
;(Ⅱ)当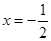 时,
时, 最小值为
最小值为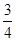 ;(Ⅲ)当
;(Ⅲ)当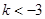 时,
时,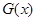 在
在 上的最大值为0;当
上的最大值为0;当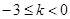 时,
时,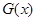 在
在 上的最大值为
上的最大值为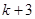 ;当
;当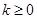 时,
时,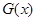 在
在 上的最大值为
上的最大值为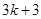 .
.试题分析:(Ⅰ)将函数
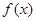 去掉绝对值写成分段函数形式,结合函数图像满足
去掉绝对值写成分段函数形式,结合函数图像满足 的
的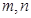 只可能为
只可能为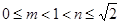 ,从而
,从而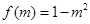 ,
,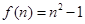 ,由
,由 即可得
即可得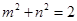 ;(Ⅱ)写出
;(Ⅱ)写出 的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为
的表达式,根据分段函数的性质,先求出每一段上的最小值,其中最小的即为  的最小值;(Ⅲ)将
的最小值;(Ⅲ)将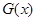 写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.
写成分段函数的形式,每一段均为二次函数的形式,结合二次函数图像,分类讨论函数的对称轴与区间的关系,从而求出最大值.试题解析:(Ⅰ)
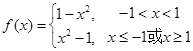
由
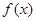 图像可知,
图像可知,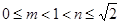
 即为
即为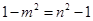 ,所以
,所以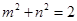 3分
3分(Ⅱ)
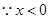 ,则
,则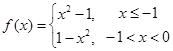 ,
,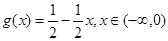
当
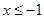 时,
时,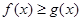 ,即为
,即为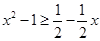 ,解得
,解得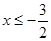
当
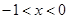 时,
时,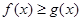 ,即为
,即为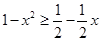 ,解得
,解得
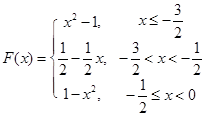
当
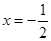 时,
时, 最小值为
最小值为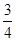
(本问也可直接利用图像说明理由求解) 6分
(Ⅲ)
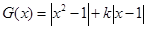
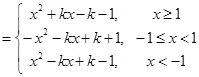
①记
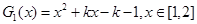 ,结合图像可知,
,结合图像可知,当
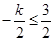 ,即
,即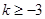 时,
时,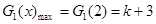
当
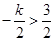 ,即
,即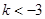 时,
时,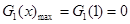 8分
8分②记
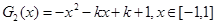 ,结合图像可知,
,结合图像可知,当
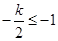 ,即
,即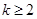 时,
时,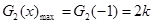
当
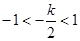 ,即
,即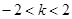 时,
时,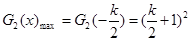
当
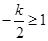 ,即
,即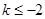 时,
时,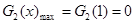
③记
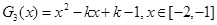 ,结合图像可知,
,结合图像可知,当
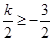 ,即
,即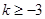 时,
时,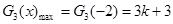
当
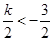 ,即
,即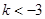 时,
时,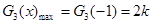 10分
10分由上讨论可知:
当
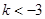 时,
时,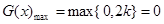
当
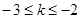 时,
时,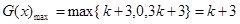
当
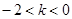 时,
时,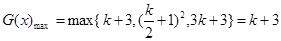
当
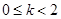 时,
时,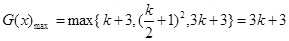
当
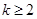 时,
时,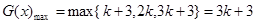 15分
15分综上所述:当
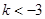 时,
时,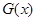 在
在 上的最大值为0
上的最大值为0当
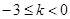 时,
时,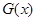 在
在 上的最大值为
上的最大值为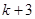
当
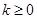 时,
时,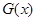 在
在 上的最大值为
上的最大值为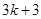 . 16分
. 16分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
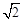 ),则
),则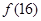 = .
= .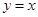 为同一函数的是
为同一函数的是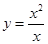
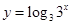
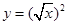
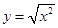
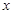 元,
元,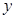 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格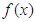 =
=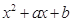 ,
,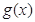 =
=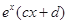 ,若曲线
,若曲线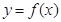 和曲线
和曲线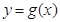 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线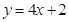 .
.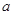 ,
,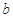 ,
,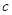 ,
,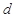 的值;
的值;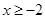 时,
时,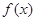 ≤
≤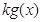 ,求
,求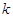 的取值范围.
的取值范围.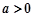 ,
,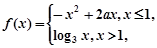 方程
方程 有且仅有两个不等实根,且较大的实根大于3,则实数
有且仅有两个不等实根,且较大的实根大于3,则实数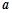 的取值范围____.
的取值范围____.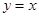 与
与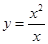 ②
②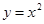 与
与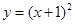
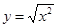 与
与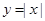 ④
④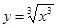
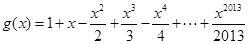 ,则函数
,则函数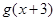 的零点所在的区间为
的零点所在的区间为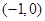
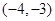
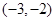 或
或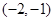
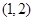
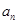 }定义如下:
}定义如下: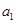 =1,当
=1,当 时,
时,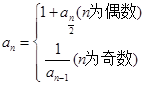 ,若
,若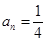 ,则
,则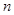 的值等于( )
的值等于( )