题目内容
已知函数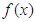 =
=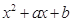 ,
,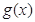 =
=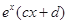 ,若曲线
,若曲线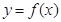 和曲线
和曲线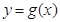 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线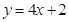 .
.
(Ⅰ)求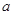 ,
,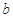 ,
,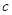 ,
,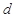 的值;
的值;
(Ⅱ)若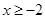 时,
时,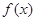 ≤
≤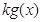 ,求
,求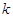 的取值范围.
的取值范围.
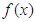 =
=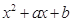 ,
,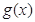 =
=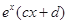 ,若曲线
,若曲线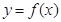 和曲线
和曲线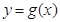 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线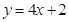 .
.(Ⅰ)求
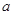 ,
,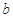 ,
,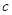 ,
,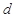 的值;
的值;(Ⅱ)若
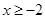 时,
时,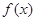 ≤
≤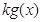 ,求
,求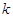 的取值范围.
的取值范围.(Ⅰ) =4,
=4, =2,
=2, =2,
=2, =2;(Ⅱ)
=2;(Ⅱ)
 =4,
=4, =2,
=2, =2,
=2, =2;(Ⅱ)
=2;(Ⅱ)
试题分析:(Ⅰ)求四个参数的值,需寻求四个独立的条件,依题意
 代入即可求出
代入即可求出 的值;(Ⅱ)构造函数,转化为求函数的最值,记
的值;(Ⅱ)构造函数,转化为求函数的最值,记 =
= =
= (
( ),由已知
),由已知 ,只需令
,只需令 的最小值大于0即可,先求
的最小值大于0即可,先求 的根,得
的根,得
 ,只需讨论
,只需讨论 和定义域
和定义域 的位置,分三种情况进行,当
的位置,分三种情况进行,当 时,将定义域分段,分别研究其导函数
时,将定义域分段,分别研究其导函数 的符号,进而求最小值;当
的符号,进而求最小值;当 时,
时, 的符号确定,故此时函数
的符号确定,故此时函数 具有单调性,利用单调性求其最小值即可.
具有单调性,利用单调性求其最小值即可.试题解析:(Ⅰ)由已知得
 ,而
,而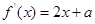

 ,代入得
,代入得 ,故
,故 =4,
=4, =2,
=2, =2,
=2, =2;
=2;(Ⅱ)由(Ⅰ)知

 ,
,设函数
 =
= =
= (
( ),
),  =
= =
= , 由题设知
, 由题设知 ,即
,即 ,令
,令 ,得
,得
 ,
,(1)若
 ,则
,则 ,∴当
,∴当 时,
时, ,当
,当 时,
时, ,记
,记 在
在 时单调递减,
时单调递减, 时单调递增,故
时单调递增,故 在
在 时取最小值
时取最小值 ,而
,而

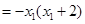
 ,∴当
,∴当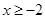 时,
时, ,即
,即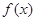 ≤
≤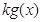 ;
;(2)若
 ,则
,则 ,∴当
,∴当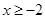 时,
时, ,∴
,∴ 在
在 单调递增,而
单调递增,而 .∴当
.∴当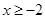 时,
时, ,即
,即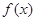 ≤
≤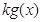 ;
;(3)若
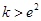 时,
时, ,则
,则 在
在 单调递增,而
单调递增,而 =
= =
=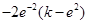 <0,
<0, ∴当
 ≥-2时,
≥-2时, ≤
≤ 不可能恒成立,
不可能恒成立, 综上所述,
 的取值范围为[1,
的取值范围为[1, ].
].
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, .
. ,若
,若 ,求
,求 的值;
的值; ,当
,当 时,求
时,求 在
在 上的最小值;
上的最小值; 在区间
在区间 上的最大值.
上的最大值.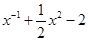 ,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1). 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
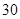 天内每件的销售价格
天内每件的销售价格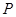 (元)与时间
(元)与时间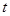 (天)的函数关系是
(天)的函数关系是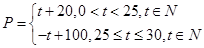 该商品的日销售量
该商品的日销售量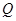 (件)与时间
(件)与时间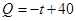
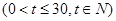 ,设商品的日销售额为
,设商品的日销售额为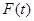 (销售量与价格之积)
(销售量与价格之积) 的定义域为
的定义域为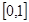 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:① ;②对任意的
;②对任意的 ,都有
,都有 ;③当
;③当 时总有
时总有 .
. 的值;
的值; 时,恒有
时,恒有 .
. ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段是股价延续
段是股价延续
 。现在老张决定取点
。现在老张决定取点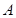
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
,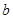 ,
, ,
, ,并且求得
,并且求得 。
。 ]
] ]
] ]
]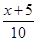 ]
] ,其中
,其中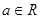 ,若对任意的非零实数
,若对任意的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 成立,则k的最小值为( )
成立,则k的最小值为( )