题目内容

1．“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如表所示：
价格x55.56.57
销售量y121064
通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
（1）求销售量y对奶茶的价格x的回归直线方程；
（2）欲使销售量为13杯，则价格应定为多少？

分析 （1）首先做出两组数据的平均数，利用最小二乘法得到线性回归方程的系数，写出线性回归方程；
（2）令-4x+32=13，可预测销销售量为13杯时的售价．

解答 解：（1）由题意知$\overline{x}$=6，$\overline{y}$=8，$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=182，$\sum_{i=1}^{4}{{x}_{i}}^{2}-4{\overline{x}}^{2}$=25，
∴b=-4，a=8+4×6=32，
∴线性回归方程是y=-4x+32；
（2）令-4x+32=13，可得x=4.75，
∴预测销售量为13杯，则价格应定为4.75元．

点评 本题考查可线性化的回归分析，考查求线性回归方程，是一个基础题．

练习册系列答案
相关题目
17．甲、乙两同学5次综合评测的成绩如茎叶图所示．老师发现乙同学成绩的一个数字无法看清．但老师知道乙的平均成绩超过甲的平均成绩，则看不清楚的数字为9．
12．已知F1，F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的两个焦点，点P是该双曲线和圆x2+y2=a2+b2的一个交点，若sin∠PF1F2=3sin∠PF2F1，则该双曲线的离心率是（　　）
A．$\frac{{\sqrt{10}}}{4}$B．$\frac{{\sqrt{10}}}{2}$C．$\sqrt{10}$D．$\sqrt{5}$
9．一辆家庭轿车在x年的使用过程中需要如下支出：购买时花费12万元；保险费，养路费，燃油费等各种费用每年1.05万元，维修费用共0.05x2+0.15x万元；使用x年后，轿车的价值为（10.75-0.8x）万元．设这辆家庭轿车的年平均支出为y万元，则由以上条件，解答以下问题：
（1）写出y关于的函数关系式；
（2）试确定一辆家庭轿车使用多少年时年平均支出最低．并求出这个最低支出．
16．在极坐标系中，圆C的方程为ρ=4$\sqrt{2}cos（θ-\frac{π}{4}）$，以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系，直线l的方程为ρsin（$\frac{π}{4}$-θ）=$\sqrt{2}$，求直线l被圆C截得的弦AB的长度．
6．求适合下列等式的x与y（x，y∈R）的值：（$\frac{1}{2}$x+y）+（5x+$\frac{2}{3}$y）i=-4+16i．
13．在复平面内，复数$\frac{{i}^{2015}}{1+i}$对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
10．已知函数f（x）=lnx-ax+1，a是常数，a∈R．
（Ⅰ）求曲线y=f（x）在点-处的切线P（1，f（1））的方程；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）证明：函数f（x）（x≠1）的图象在直线l的下方．
11．如图所示的程序框图中，若x=5，则输出i的值是（　　）
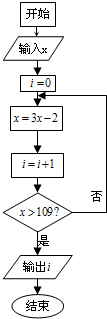
A．2B．3C．4D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网