题目内容
13．在复平面内，复数$\frac{{i}^{2015}}{1+i}$对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的代数形式的混合运算化简求解即可．
解答 解：复数$\frac{{i}^{2015}}{1+i}$=$\frac{-i}{1+i}$=$\frac{-i（1-i）}{（1+i）（1-i）}$=$\frac{-1-i}{2}$=$-\frac{1}{2}$$-\frac{1}{2}$i．
复数对应点为（$-\frac{1}{2}，-\frac{1}{2}$）在第三象限．
故选：C，
点评 本题考查复数的代数形式的混合运算，复数的几何意义，考查计算能力．
练习册系列答案
相关题目
1．“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如表所示：
通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
（1）求销售量y对奶茶的价格x的回归直线方程；
（2）欲使销售量为13杯，则价格应定为多少？
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
（1）求销售量y对奶茶的价格x的回归直线方程；
（2）欲使销售量为13杯，则价格应定为多少？
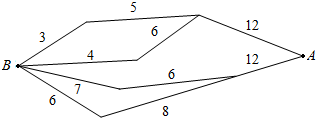如图，标注的数字表示该段网线单位时间内可以通过的最大信息量，现从结点A向结点B传递信息，信息可以分开沿不同的路线同时传递，小圆圈表示网络的结点，结点之间的连线表示他们有网线相连，则单位时间内传递的最大信息量为（ ）