题目内容
16.在极坐标系中,圆C的方程为ρ=4$\sqrt{2}cos(θ-\frac{π}{4})$,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,直线l的方程为ρsin($\frac{π}{4}$-θ)=$\sqrt{2}$,求直线l被圆C截得的弦AB的长度.分析 把圆C、直线l的极坐标方程都化为普通方程;求出圆心C到直线l的距离,利用勾股定理求出弦长AB的值.
解答 解:∵圆C的方程为ρ=4$\sqrt{2}$cos(θ-$\frac{π}{4}$),
∴ρ=4cosθ+4sinθ,
两边同乘以ρ,得:
ρ2=4ρcosθ+4ρsinθ,
∴普通方程为x2+y2-4x-4y=0,
其圆心C的坐标为(2,2),半径r=2$\sqrt{2}$;
又直线l的方程为ρsin($\frac{π}{4}$-θ)=$\sqrt{2}$,
化为普通方程是x-y-2=0;
∴圆心C到直线l的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴弦长AB=2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{8-2}$=2$\sqrt{6}$.
点评 本题考查了极坐标方程化为普通方程的应用问题,也考查了直线与圆的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如表所示:
通过分析,发现销售量y对奶茶的价格x具有线性相关关系.
(1)求销售量y对奶茶的价格x的回归直线方程;
(2)欲使销售量为13杯,则价格应定为多少?
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
(1)求销售量y对奶茶的价格x的回归直线方程;
(2)欲使销售量为13杯,则价格应定为多少?
8.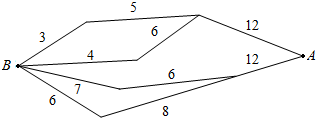 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
 如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )
如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的最大信息量为( )| A. | 26 | B. | 24 | C. | 20 | D. | 19 |
6.已知集合M={x|(x-1)2≤4}和N={x|x=2k-1,k∈N*},则M∩N=( )
| A. | {1,3} | B. | [1,5) | C. | {1,3,5} | D. | ∅ |