题目内容
设命题p:函数 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对一切实数均成立。
对一切实数均成立。
(1)如果p是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数 的取值范围。
的取值范围。
 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对一切实数均成立。
对一切实数均成立。(1)如果p是真命题,求实数
 的取值范围;
的取值范围;(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数
 的取值范围。
的取值范围。(1) ;(2)
;(2)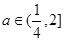
 ;(2)
;(2)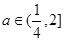
试题分析:(1)求函数
 的定义域为R只需满足
的定义域为R只需满足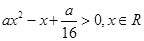 恒成立即可.(2)命题“p或q”为真命题,且“p且q”为假命题即p和q一真一假,p真q假或p假q真.
恒成立即可.(2)命题“p或q”为真命题,且“p且q”为假命题即p和q一真一假,p真q假或p假q真.试题解析:(1)若命题p为真命题,则
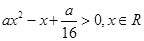 恒成立
恒成立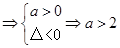
(2)若命题q为真命题,则
 ;
;“p或q”为真命题且“p且q”为假命题,即p,q一真一假 故
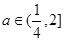 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .设
.设 方程
方程 有实数根;
有实数根; 函数
函数 在区间
在区间 上是增函数.若
上是增函数.若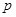 和
和 有且只有一个正确,求实数
有且只有一个正确,求实数 的取值范围.
的取值范围. =-1
=-1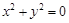 ,则
,则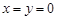 ”,在它的逆命题、否命题、逆否命题中,真命题的个数是
”,在它的逆命题、否命题、逆否命题中,真命题的个数是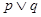 ”为真命题,则下列命题一定为假命题的是( )
”为真命题,则下列命题一定为假命题的是( )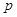
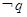
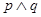
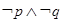

 ,
,

 ”为假命题,则实数
”为假命题,则实数 的取值范围为 .
的取值范围为 .