题目内容
如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;

(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;

以D为坐标原点,直线DA,DC,DD1分别为x, y, z轴,建立空间直角坐标系,设AE=x,则A1(1,0,1),D1(0,0,1),
E(1,x,0),A(1,0,0),C(0,2,0)
(1)证明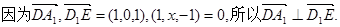

(2)解 因为E为AB的中点,则E(1,1,0),
从而 ,
,
 ,
,
设平面ACD1的法向量为 ,
,
则
也即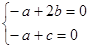 ,得
,得 ,从而
,从而 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为

E(1,x,0),A(1,0,0),C(0,2,0)
(1)证明
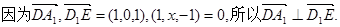

(2)解 因为E为AB的中点,则E(1,1,0),
从而
 ,
, ,
,设平面ACD1的法向量为
 ,
,则

也即
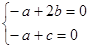 ,得
,得 ,从而
,从而 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的正方体
的正方体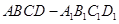 中,
中,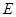 是线段
是线段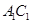 的中点,
的中点, .
.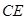 ^
^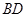 ;
;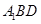 ;
;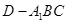 的表面积.
的表面积.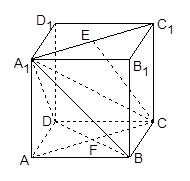
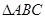 沿
沿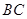 边上的高
边上的高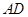 折成直二面角
折成直二面角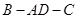 ,则三棱锥
,则三棱锥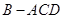 的外接球的表面积为 _________
的外接球的表面积为 _________
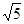 ,BC=AD=
,BC=AD=
 中,
中,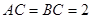 ,
, ,
,  ,点
,点 的中点,
的中点,
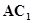 //平面
//平面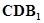 ;
;  的体积.
的体积.
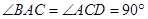 ,AE∥C
,AE∥C D,DC=AC=2AE=2.
D,DC=AC=2AE=2.
 平面ABC
平面ABC