题目内容
如图,矩形ABCD中,AB=CD=2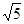 ,BC=AD=
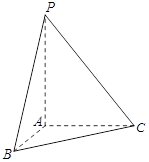
,BC=AD=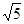 。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积;
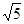 ,BC=AD=
,BC=AD=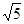 。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。(Ⅰ)求二面角A—BD—C平面角的余弦值。
(Ⅱ)求四面体ABCD外接球的体积;

如图,过点D、B分别向AC引垂线,垂足分别为E、F。易知AE=CF=1,EF=3,DE=BF=2。又DE⊥AC,AC=面ACD∩面ABC,二面角D—AC—B为直二面角,所以DE⊥平面ABC,又因为BF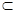 平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
则各点的如下A(0,-4,0),B(2,0,0),C(0,1,0),D(0,-3,2). (3分)
(1)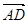 =(0,1,2),
=(0,1,2),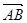 =(2,4,0),
=(2,4,0),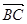 =(-2,1,0),
=(-2,1,0),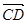 =(0,-4,2)
=(0,-4,2)
设平面ABD的法向量为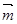 =(x,y,1),则
=(x,y,1),则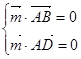
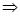
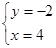 ,
,
即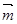 =(4,-2,1)
=(4,-2,1)
设平面BCD的法向量为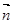 =(1,b,c),则
=(1,b,c),则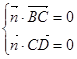
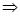
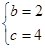
即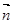 =(1,2,4)
=(1,2,4)
Cos<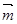 ,
,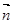 >=
>=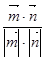 =
=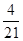 .
.
由图形知二面角A—BD—C平面角的余弦值为-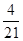 . (8分)
. (8分)
(2)设O为AC的中点,∵⊿ABC与⊿ADC都为直角三角形,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心.
∴四面体ABCD的体积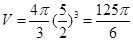
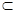 平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.
平面ABC,所以DE⊥BF。故DE、AC、BF两两垂直。如图以点F为坐标原点,FB为x轴,FC为y轴,平行于ED的方向为z轴,建立空间直角坐标系.则各点的如下A(0,-4,0),B(2,0,0),C(0,1,0),D(0,-3,2). (3分)
(1)
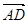 =(0,1,2),
=(0,1,2),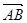 =(2,4,0),
=(2,4,0),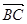 =(-2,1,0),
=(-2,1,0),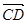 =(0,-4,2)
=(0,-4,2)设平面ABD的法向量为
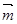 =(x,y,1),则
=(x,y,1),则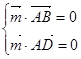
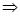
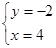 ,
,即
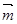 =(4,-2,1)
=(4,-2,1)设平面BCD的法向量为
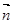 =(1,b,c),则
=(1,b,c),则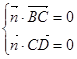
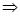
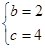
即
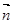 =(1,2,4)
=(1,2,4)Cos<
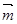 ,
,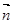 >=
>=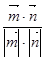 =
=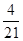 .
. 由图形知二面角A—BD—C平面角的余弦值为-
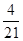 . (8分)
. (8分)(2)设O为AC的中点,∵⊿ABC与⊿ADC都为直角三角形,∴OA=OB=OC=OD,∴O为四面体ABCD的外接球的球心.
∴四面体ABCD的体积
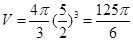
略

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
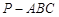 ,
,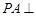 平面
平面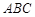 ,
,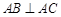 ,
,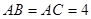 ,
,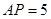 .
.
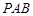 (及其内部)绕
(及其内部)绕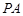 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积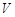 ;
; 的余弦值.
的余弦值.

 满足
满足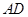 ∥
∥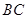 ,
,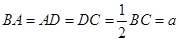 ,
,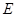 是
是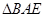 沿着
沿着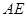 翻折成
翻折成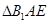 ,使面
,使面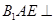 面
面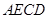 ,
,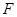 为
为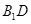 的中点.
的中点. 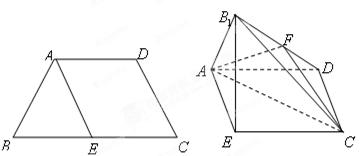
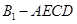 的体积;
的体积;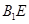 ∥面
∥面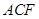 ;
;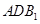 与面
与面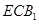 所成二面角的余弦值.
所成二面角的余弦值.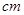 ),则这个几何体的体积为( )
),则这个几何体的体积为( )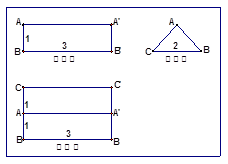

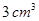
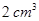
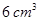
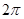 ,底面面积为
,底面面积为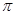 ,则该圆锥的体积为 。
,则该圆锥的体积为 。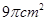 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为
,且它的侧面展开图是一个半圆,则圆锥的底面半径为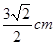

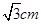
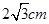 ()
()