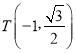题目内容
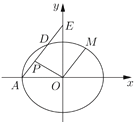
【题目】如图,已知△![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,且
,且![]() ,延长线段
,延长线段![]() 到点
到点![]() ,使得
,使得![]() ,
,![]() .
.
(1)求证:![]() 是直角;
是直角;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据正弦定理以及二倍角公式即可证明,
(2)如图所示:过点C作CE⊥AC,根据平行线分线段成比例定理,设CE=x,则AB=5x,AD![]() x,再根据勾股定理可得x的值,再由正弦定理,sinD
x,再根据勾股定理可得x的值,再由正弦定理,sinD![]() ,再根据同角的三角函数的关系即可求出答案.
,再根据同角的三角函数的关系即可求出答案.
1)由正弦定理可得sinBcosB=sinCcosC,
即sin2B=sin2C,
∵b≠c,
∴2B+2C=180°,
∴B+C=90°,
∴∠BAC=180°﹣90°=90°,
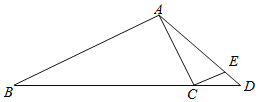
(2)如图所示:过点C作CE⊥AC,
∵BC=4,BC=4CD,
∴CD=1,BD=5,
∵∠BAC=90°,
∴CE∥AB,
∴![]() ,
,
设CE=x,则AB=5x,
∵∠CAD=30°,
∴AE=2x,AC![]() x,
x,
∴![]() ,
,
∴DE![]() x,
x,
∵AB2+AC2=BC2,
∴25x2+3x2=16,
解得x![]() ,
,
在△CED中,∠CED=120°,CE![]() ,CD=1,
,CD=1,
由正弦定理可得![]() ,
,
即sinD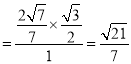 ,
,
cosD![]() ,
,
∴tanD![]() .
.

练习册系列答案
相关题目