题目内容
【题目】数列![]() 满足
满足![]() ,
,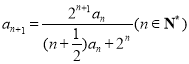 .
.
(1)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)由已知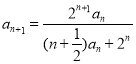 ,得
,得 ,
,
即![]() ,即
,即![]() ,即
,即![]() .(2分)
.(2分)
所以![]() ,
,![]() ,…,
,…,![]() ,
,
以上各式相加得![]() .
.
又![]() ,所以
,所以![]() .(5分)
.(5分)
(2)由(1)知![]() ,所以
,所以![]() ,
,
![]()
![]()
![]()
![]() .(7分)
.(7分)
所以![]()
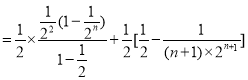
![]()
![]() .(10分)
.(10分)
【易错提醒】(1)对递推式变形时,应明确方向,准确把握数列的递推关系,通过变形将其转化为常见的等差、等比数列问题求解是解决此类问题的基本思路;(2)构造新数列时,一定要注意原数列的项与新数列的项之间的对应,如本题中第(1)问,![]() ,则
,则![]() 的表达式既不是
的表达式既不是![]() ,也不是
,也不是![]() ,而是
,而是![]() ,即把式子中所有的
,即把式子中所有的![]() 都换成
都换成![]() .
.
【解题技巧】求解数列递推关系式问题的基本原则就是对数列的递推式进行变换,把原问题转换为等差、等比数列进行处理.转化的常用方法有:(1)待定系数法,如![]() ,可以通过待定系数
,可以通过待定系数![]() 将其转化为形如
将其转化为形如![]() 的等比数列;(2)取倒数法,如本题;(3)观察变换法,如
的等比数列;(2)取倒数法,如本题;(3)观察变换法,如![]() ,可以在两端同时除以
,可以在两端同时除以![]() ,转化为形如
,转化为形如![]() 的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.
的等差数列;(4)取对数法等.求解数列递推关系式问题要注意选取合适的变换递推式的方法,通过变换进行解答,在变换时要小心谨慎.

练习册系列答案
相关题目
【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1 | y2 | |
x1 | a | 20-a |
x2 | 15-a | 30+a |
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?