МвДїДЪИЭ
ЎѕМвДїЎїДіѕ°ЗшРЮЅЁТ»¶°ёґ№ЕЅЁЦюЈ¬Ждґ°»§ЙијЖИзНјЛщКѕ.ФІ![]() µДФІРДУлѕШРО
µДФІРДУлѕШРО![]() ¶ФЅЗПЯµДЅ»µгЦШєПЈ¬ЗТФІУлѕШРОЙППВБЅ±ЯПаЗРЈЁ
¶ФЅЗПЯµДЅ»µгЦШєПЈ¬ЗТФІУлѕШРОЙППВБЅ±ЯПаЗРЈЁ![]() ОЄЙПЗРµгЈ©Ј¬УлЧуУТБЅ±ЯПаЅ»ЈЁ
ОЄЙПЗРµгЈ©Ј¬УлЧуУТБЅ±ЯПаЅ»ЈЁ![]() Ј¬
Ј¬![]() ОЄЖдЦРБЅёцЅ»µгЈ©Ј¬НјЦРТхУ°Ії·ЦОЄІ»Нё№вЗшУтЈ¬ЖдУаІї·ЦОЄНё№вЗшУт.ТСЦЄФІµД°лѕ¶ОЄ1
ОЄЖдЦРБЅёцЅ»µгЈ©Ј¬НјЦРТхУ°Ії·ЦОЄІ»Нё№вЗшУтЈ¬ЖдУаІї·ЦОЄНё№вЗшУт.ТСЦЄФІµД°лѕ¶ОЄ1![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬Йи
Ј¬Йи![]() Ј¬Нё№вЗшУтµДГж»эОЄ
Ј¬Нё№вЗшУтµДГж»эОЄ![]() .
.
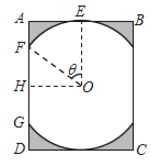
ЈЁ1Ј©Зу![]() №ШУЪ
№ШУЪ![]() µДєЇКэ№ШПµКЅЈ¬ІўЗуіц¶ЁТеУтЈ»
µДєЇКэ№ШПµКЅЈ¬ІўЗуіц¶ЁТеУтЈ»
ЈЁ2Ј©ёщѕЭЙијЖТЄЗуЈ¬Нё№вЗшУтУлѕШРОґ°ГжµДГж»э±ИЦµФЅґуФЅєГ.µ±ёГ±ИЦµЧоґуК±Ј¬Зу±Я![]() µДі¤¶И.
µДі¤¶И.
Ўѕґр°ёЎїЈЁ1Ј©![]() №ШУЪ
№ШУЪ![]() µДєЇКэ№ШПµКЅОЄ
µДєЇКэ№ШПµКЅОЄ![]() Ј¬¶ЁТеУтОЄ
Ј¬¶ЁТеУтОЄ![]() Ј»
Ј»
ЈЁ2Ј©Нё№вЗшУтУлѕШРОґ°ГжµДГж»э±ИЦµЧоґуК±Ј¬![]() µДі¤¶ИОЄ1
µДі¤¶ИОЄ1![]() Ј®
Ј®
ЎѕЅвОцЎїКФМв·ЦОцЈє
(1) №эµг![]() Чч
Чч![]() УЪµг
УЪµг![]() Ј¬їЙµГ
Ј¬їЙµГ![]() №ШУЪ
№ШУЪ![]() µДєЇКэ№ШПµКЅОЄ
µДєЇКэ№ШПµКЅОЄ![]() Ј¬¶ЁТеУтОЄ
Ј¬¶ЁТеУтОЄ![]() Ј»
Ј»
(2)УЙФєЇКэУлµјєЇКэµД№ШПµїЙµГµ±![]() К±Ј¬
К±Ј¬![]() УРЧоґуЦµ
УРЧоґуЦµ![]() Ј¬ґЛК±
Ј¬ґЛК±![]()
КФМвЅвОцЈє
Ѕв:(1) №эµг![]() Чч
Чч![]() УЪµг
УЪµг![]() Ј¬Фт
Ј¬Фт![]() Ј¬
Ј¬
ЛщТФ![]() Ј¬
Ј¬
![]() Ј®
Ј®
ЛщТФ![]()
![]()
![]() Ј¬
Ј¬
ТтОЄ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ¶ЁТеУтОЄ
Ј¬ЛщТФ¶ЁТеУтОЄ![]() Ј®
Ј®
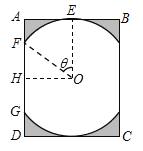
ЈЁ2Ј©ѕШРОґ°ГжµДГж»эОЄ![]() Ј®
Ј®
ФтНё№вЗшУтУлѕШРОґ°ГжµДГж»э±ИЦµОЄ![]() Ј®
Ј®
Йи![]() Ј¬
Ј¬![]() Ј®
Ј®
Фт![]()
![]()
![]()
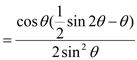 Ј¬
Ј¬
ТтОЄ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬№К
Ј¬№К![]() Ј¬
Ј¬
ЛщТФєЇКэ![]() ФЪ
ФЪ![]() ЙПµҐµчјхЈ®
ЙПµҐµчјхЈ®
ЛщТФµ±![]() К±Ј¬
К±Ј¬![]() УРЧоґуЦµ
УРЧоґуЦµ![]() Ј¬ґЛК±
Ј¬ґЛК±![]()
ґрЈєЈЁ1Ј©![]() №ШУЪ
№ШУЪ![]() µДєЇКэ№ШПµКЅОЄ
µДєЇКэ№ШПµКЅОЄ![]() Ј¬¶ЁТеУтОЄ
Ј¬¶ЁТеУтОЄ![]() Ј»
Ј»
ЈЁ2Ј©Нё№вЗшУтУлѕШРОґ°ГжµДГж»э±ИЦµЧоґуК±Ј¬![]() µДі¤¶ИОЄ1
µДі¤¶ИОЄ1![]() Ј®
Ј®

ЎѕМвДїЎїУРБЅёц·ЦАа±дБїxУлyЈ¬ЖдТ»Чй№ЫІвЦµИзПВГжµД2ЎБ2БРБЄ±нЛщКѕЈє
y1 | y2 | |
x1 | a | 20Јa |
x2 | 15Јa | 30Ј«a |
ЖдЦРa,15ЈaѕщОЄґуУЪ5µДХыКэЈ¬ФтaИЎєОЦµК±Ј¬ФЪ·ёґнОуµДёЕВКІ»і¬№э0.1µДЗ°МбПВИПОЄxУлyЦ®јдУР№ШПµЈї