题目内容

8．已知函数f（x）=4x2-mx+1在（-∞，-2]上递减，在[-2，+∞）上递增，则f（1）=（　　）
A．19B．20C．21D．22

分析 根据已知可得函数的对称轴x=$\frac{m}{8}$=-2，求出m值后，可得函数的解析式，将x=1代入可得答案．

解答 解：∵函数f（x）=4x2-mx+1在（-∞，-2]上递减，在[-2，+∞）上递增，
∴$\frac{m}{8}$=-2，
解得：m=-16，
∴f（x）=4x2+16x+1，
∴f（1）=21，
故选：C．

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
18．若函数$f（x）={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{2014}}{x^{2014}}（x∈R）$是奇函数，则a0+a2+a4+…+a2014=0．
19．已知一个圆C经过两个点A（6，-2），B（-1，5），且圆心在直线l：x-2y+1=0上，求此圆的标准方程．
16．已知集合$A=\left\{{x{{\left|{（{\frac{1}{2}}）}\right.}^x}＞1}\right\}$，集合B={x|lgx＜0}则A∩B（　　）
A．{x|x＜0}B．{x|0＜x＜1}C．{x|x＞1}D．φ
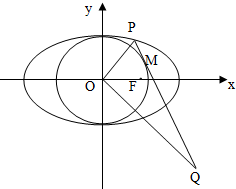3．在平面直角坐标系xoy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右焦点F（1，0），点P在椭圆C上，且在第一象限内，直线PQ与圆O：x2+y2=b2相切于点M．
（1）求椭圆C的方程；
（2）若|PM|×|PF|=$\frac{3}{4}$，求点P的横坐标的值；
（3）若OP⊥OQ，求点Q的纵坐标t的值．
13．抛物线C：y2=2x的准线方程是x=-$\frac{1}{2}$，经过点P（4，1）的直线l与抛物线C相交于A，B两点，且点P恰为AB的中点，F为抛物线的焦点，则$|{\overrightarrow{AF}}|+|{\overrightarrow{BF}}|$=9．
20．已知-1＜a＜b＜2，则2a-b的范围是（-4，2）．
17．已知A={x|a＜x＜3+a}，B={x|x≤-1或x≥1}；
（1）若A∪B=R，求实数a的取值范围；
（2）若A⊆B，求实数a的取值范围．
18．若a＜b＜0，则（　　）
A．a2＜ab＜b2B．ac＜bcC．$\frac{1}{a}＞\frac{1}{b}$D．$\frac{a}{c^2}＞\frac{b}{c^2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网