Question

【题目】[选修4-4：坐标系与参数方程选讲]

已知曲线C1的极坐标方程为ρ2cos2θ=8，曲线C2的极坐标方程为 ，曲线C1、C2相交于A、B两点．
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）曲线C1与直线 （t为参数）分别相交于M，N两点，求线段MN的长度．

Answer 1

【答案】解：（Ⅰ）由ρ2cos2θ=8，曲线C2的极坐标方程为 ，可得ρ=±4，
∴A、B两点的极坐标分别为（4， ），（4，﹣ ）；
（Ⅱ）由ρ2cos2θ=8，得直角坐标方程为x2﹣y2=8，
直线 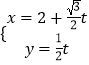（t为参数），代入整理可得t2+4 ﹣8=0，
∴|MN|= =4 ．
【解析】（Ⅰ）由ρ2cos2θ=8，曲线C2的极坐标方程为 ，可得ρ=±4，即可求A、B两点的极坐标；（Ⅱ）由ρ2cos2θ=8，得直角坐标方程为x2﹣y2=8，直线 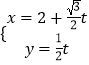（t为参数），代入整理可得t2+4 ﹣8=0，利用弦长公式求线段MN的长度．