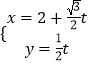题目内容
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() .
.
(1)写出C1的普通方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.
【答案】
(1)
解:曲线C1的参数方程为 ![]() (α为参数),
(α为参数),
移项后两边平方可得 ![]() +y2=cos2α+sin2α=1,
+y2=cos2α+sin2α=1,
即有椭圆C1: ![]() +y2=1;
+y2=1;
曲线C2的极坐标方程为ρsin(θ+ ![]() )=2
)=2 ![]() ,
,
即有ρ( ![]() sinθ+
sinθ+ ![]() cosθ)=2
cosθ)=2 ![]() ,
,
由x=ρcosθ,y=ρsinθ,可得x+y﹣4=0,
即有C2的直角坐标方程为直线x+y﹣4=0;
(2)
解:由题意可得当直线x+y﹣4=0的平行线与椭圆相切时,
|PQ|取得最值.
设与直线x+y﹣4=0平行的直线方程为x+y+t=0,
联立 ![]() 可得4x2+6tx+3t2﹣3=0,
可得4x2+6tx+3t2﹣3=0,
由直线与椭圆相切,可得△=36t2﹣16(3t2﹣3)=0,
解得t=±2,
显然t=﹣2时,|PQ|取得最小值,
即有|PQ|= ![]() =
= ![]() ,
,
此时4x2﹣12x+9=0,解得x= ![]() ,
,
即为P( ![]() ,
, ![]() ).
).
另解:设P( ![]() cosα,sinα),
cosα,sinα),
由P到直线的距离为d= ![]()
= ![]() ,
,
当sin(α+ ![]() )=1时,|PQ|的最小值为
)=1时,|PQ|的最小值为 ![]() ,
,
此时可取α= ![]() ,即有P(
,即有P( ![]() ,
, ![]() ).
).
【解析】(1)运用两边平方和同角的平方关系,即可得到C1的普通方程,运用x=ρcosθ,y=ρsinθ,以及两角和的正弦公式,化简可得C2的直角坐标方程;(2)由题意可得当直线x+y﹣4=0的平行线与椭圆相切时,|PQ|取得最值.设与直线x+y﹣4=0平行的直线方程为x+y+t=0,代入椭圆方程,运用判别式为0,求得t,再由平行线的距离公式,可得|PQ|的最小值,解方程可得P的直角坐标.
另外:设P( ![]() cosα,sinα),由点到直线的距离公式,结合辅助角公式和正弦函数的值域,即可得到所求最小值和P的坐标.
cosα,sinα),由点到直线的距离公式,结合辅助角公式和正弦函数的值域,即可得到所求最小值和P的坐标.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案