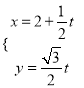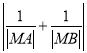题目内容
【题目】已知各项都为正数的数列{an}满足a1＝1， 
＝2an＋1(an＋1)－an.
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)设bn＝
，求数列{an·bn}的前n项和Tn.
【答案】(Ⅰ)an＝(
)n－1(Ⅱ)Tn＝2－(n＋1)( 
)n－1.
【解析】试题分析：(Ⅰ)由
＝2an＋1(an＋1)－an，化简可得
.进而可得an＝(
)n－1.
(Ⅱ) 根据错位相减法，即可求出数列的数列{an·bn}的前n项和Tn.
试题解析：(Ⅰ)由
＝2an＋1(an＋1)－an，
得2an＋1(an＋1)＝an(an＋1)，
因为数列{an}的各项都为正数，所以
.
故数列{an}是首项为1，公比为
的等比数列，因此an＝(
)n－1.
(Ⅱ)由(Ⅰ)知an＝(
)n－1，故bn＝n－1，所以an·bn＝(n－1)( 
)n－1，数列{an·bn}的前n项和Tn＝
＋2×(
)2＋3×(
)3＋…＋(n－2)×(
)n－2＋(n－1)×(
)n－1①
Tn＝(
)2＋2×(
)3＋3×(
)4＋…＋(n－2)×(
)n－1＋(n－1)×(
)n，②
①－②得
Tn＝
＋(
)2＋(
)3＋…＋(
)n－1－(n－1)×(
)n
＝
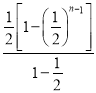－(n－1)×(
)n＝1－(
)n－1－(n－1)×(
)n＝1－(n＋1)( 
)n，
Tn＝2－(n＋1)( 
)n－1.
全能测控一本好卷系列答案
【题目】
近年来，随着双十一、双十二等网络活动的风靡，各大网商都想出了一系列的降价方案，以此来提高自己的产品利润. 已知在2016年双十一某网商的活动中，某店家采取了两种优惠方案以供选择：
方案一：购物满400元以上的，超出400元的部分只需支出超出部分的x%；
方案二：购物满400元以上的，可以参加电子抽奖活动，即从1,2,3,4,5,6这6张卡牌中任取2张，将得到的数字相加，所得结果与享受优惠如下：
数字和 | [3,4] | [5,7] | [8,9] | [10,11] |
实际付款 | 原价 | 9折 | 8折 | 5折 |
(Ⅰ)若某顾客消费了800元，且选择方案二，求该顾客只需支付640元的概率；
(Ⅱ)若某顾客购物金额为500元，她选择了方案二后，得到的数字之和为6，此时她发现使用方案一、二最后支付的金额相同，求x的值．
