Question

【题目】(导学号：05856262)

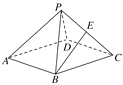
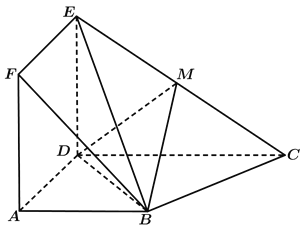
如图所示，在斜三棱柱ABC－A1B1C1中，AB＝BC＝1，AA1＝2，D是AC的中点，AB⊥平面B1C1CB，∠BCC1＝60°.

(Ⅰ)求证：AC⊥平面BDC1；

(Ⅱ)E是线段CC1上的动点，判断点E到平面AA1B1B的距离是否为定值，若是，求出此定值；否则，说明理由．

Answer 1

【答案】(1)见解析；(2)定值为

【解析】试题分析：（1）利用余弦定理易证C1B⊥BC，又平面ABC⊥平面BCC1B1所以C1B⊥平面ABC进而易得AC⊥平面BDC1（2）CC1∥平面A1B1BA，所以点E到平面A1B1BA的距离与E的位置无关，为一定值．利用等积法构建所求量的方程，解之即可.

试题解析：

(Ⅰ)在△BCC1中，BC＝BC2＋CC－2BC×CC1×cos∠BCC1＝1＋4－2×1×2×＝3，

∵CC＝BC2＋BC，∴C1B⊥BC.∵AB⊥平面BCC1B1，∴平面ABC⊥平面BCC1B1，

∴C1B⊥平面ABC，则平面BC1D⊥平面ABC.

∵AB＝BC，D是AC的中点，∴AC⊥BD，∴AC⊥平面BDC1.

(Ⅱ)∵CC1∥BB1，∴CC1∥平面A1B1BA，所以点E到平面A1B1BA的距离与E的位置无关，为一定值．

∵A1B1∥AB，∴A1B1⊥平面B1C1CB.

设点E到平面AA1BB1的距离为h，则VE－A1B1B＝VA1－B1BE.

∵S△A1B1B＝×A1B1×BB1＝×1×2＝1，

S△BB1E＝SBCC1B1＝S△BC1C＝BC1×BC＝，

∴S△A1B1B×h＝S△BB1E×A1B1，即h＝，也即点E到平面AA1B1B的距离为.