题目内容
【题目】已知函数f(x)=x2-aln x(a>0)的最小值是1.
(1)求a;
(2)若关于x的方程f2(x)ex-6mf(x)+9me-x=0在区间[1,+∞)有唯一的实根,求m的取值范围.
【答案】(1)a=2.(2) 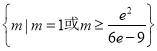 .
.
【解析】试题分析:
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出![]() 的最小值,问题转化为
的最小值,问题转化为![]() ,记
,记![]() ,根据函数的单调性求出的值即可;
,根据函数的单调性求出的值即可;
(2)由条件可得![]() ,令
,令![]() ,原问题等价于方程
,原问题等价于方程![]() 在区间
在区间![]() 内有唯一解,通过讨论
内有唯一解,通过讨论![]() 的符号,求出的范围即可.
的符号,求出的范围即可.
试题解析:
(1)f′(x)=2x-![]() =
=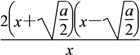 (x>0).
(x>0).
所以,当0<x<![]() 时,f′(x)<0,函数f(x)单调递减;当x>
时,f′(x)<0,函数f(x)单调递减;当x>![]() 时,f′(x)>0,函数f(x)单调递增.
时,f′(x)>0,函数f(x)单调递增.
故f(x)min=f![]() =
=![]() -
-![]() ln
ln![]() ,
,
由题意可得:![]() -
-![]() ln
ln![]() =1,即
=1,即![]() -
-![]() ln
ln![]() -1=0,
-1=0,
记g(a)=![]() -
-![]() ln
ln![]() -1(a>0),
-1(a>0),
则函数g(a)的零点即为方程![]() -
-![]() ln
ln![]() =1的根;
=1的根;
由于g′(a)=-![]() ln
ln![]() ,故a=2时,g′(2)=0,
,故a=2时,g′(2)=0,
且0<a<2时,g′(a)>0;a>2时,g′(a)<0,
所以a=2是函数g(a)的唯一极大值点,
所以g(a)≤g(2),又g(2)=0,所以a=2.
(2)由条件可得f2(x)e2x-6mf(x)ex+9m=0,
令g(x)=f(x)ex=(x2-2ln x)ex,
则g′(x)=![]() ex,
ex,
令r(x)=x2+2x-![]() -2ln x(x≥1),
-2ln x(x≥1),
则r′(x)=2x+2+![]() -
-![]() >2x-
>2x-![]() =
=![]() ≥0,
≥0,
r(x)在区间[1,+∞)内单调递增,
∴g(x)≥g(1)=e;
所以原问题等价于方程t2-6mt+9m=0在区间[e,+∞)内有唯一解,
当Δ=0时可得m=0或m=1,经检验m=1满足条件.
当Δ>0时可得m<0或m>1,
所以e2-6me+9m≤0,解之得m≥![]() ,
,
综上,m的取值范围是![]() .
.

【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 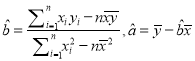 .
.
参考数据: ![]() .
.