题目内容
【题目】已知曲线C的参数方程为 ![]() (φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(φ为参数),以原点为极点,x轴的非负半轴为极轴建立极坐标系. (Ⅰ)求曲线C的极坐标方程;
(Ⅱ)已知倾斜角为135°且过点P(1,2)的直线l与曲线C交于M,N两点,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)曲线C的参数方程为 ![]() (φ为参数), 消去参数得曲线C的普通方程为x2+(y﹣3)2=9,即x2+y2﹣6y=0,
(φ为参数), 消去参数得曲线C的普通方程为x2+(y﹣3)2=9,即x2+y2﹣6y=0,
即x2+y2=6y,即ρ2=6ρsinθ,故曲线C的极坐标方程为ρ=6sinθ.
(Ⅱ)设直线  (t为参数),将此参数方程代入x2+y2﹣6y=0中,
(t为参数),将此参数方程代入x2+y2﹣6y=0中,
化简可得 ![]() ,显然△>0;
,显然△>0;
设M,N所对应的参数分别为t1 , t2 , 故  ,
,
∴ 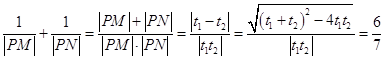
【解析】(Ⅰ)曲线C的参数方程化为普通方程x2+y2﹣6y=0,由此能求出曲线C的极坐标方程.(Ⅱ)直线  (t为参数),将此参数方程代入x2+y2﹣6y=0中,得
(t为参数),将此参数方程代入x2+y2﹣6y=0中,得 ![]() ,由此能求出
,由此能求出 ![]() 的值.
的值.

【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,
9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ;
;
(3)试预测加工10个零件需要多少时间.
参考公式:回归直线![]() ,
,
其中 ,
,![]()
