Question

【题目】已知椭圆C： + =1（a＞b＞0）经过点（0， ），离心率e= ．
（Ⅰ）求椭圆C的方程及焦距．
（Ⅱ）椭圆C的左焦点为F1 ， 右顶点为A，经过点A的直线l与椭圆C的另一交点为P．若点B是直线x=2上异于点A的一个动点，且直线BF1⊥l，问：直线BP是否经过定点？若是，求出该定点的坐标；若不是，说明理由．

Answer 1

【答案】解：（I）由题意可得：b= ， ，a2=b2+c2 ．
联立解得：a=2，c=1．
∴椭圆C的方程为： =1，焦距为2．
（II）设PA的方程为：my=x﹣2．（m≠0）．
联立 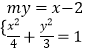，化为：（3m2+4）y2+12my=0，
解得yP= ，∴xP= ．
∴P ．
设B（2，t），则 =﹣1，解得t=﹣3m．
∴直线BP的方程为：y+3m= 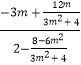（x﹣2），
化为：4y+m（6+3x）=0，令6+3x=0，4y=0，
解得x=﹣2，y=0．
∴直线BP经过定点（﹣2，0）．

【解析】（I）由题意可得：b= ， ，a2=b2+c2 ． 联立解得：a，c．即可得出椭圆C的方程及其焦距．（II）设PA的方程为：my=x﹣2．（m≠0）．与椭圆方程联立化为：（3m2+4）y2+12my=0，
解得P ．设B（2，t），根据 =﹣1，解得t=﹣3m．可得直线BP的方程为：y+3m=kBP（x﹣2），可得直线BP经过定点（﹣2，0）．