题目内容
9.已知f(x)=$\left\{\begin{array}{l}-3{x^2}+4x,0≤x<1\\ f(x-1)+1,x≥1.\end{array}\right.$,则f(3)=3;若关于x的方程f(x)=ax+1恰有三个不同的解,则实数a的取值范围为(0,$\frac{1}{2}$)∪(4-2$\sqrt{3}$,$\frac{2}{3}$).分析 作出函数f(x)和y=ax+1的图象,将方程问题转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答  解:由f(x)的表达式得f(3)=f(2)+1=f(1)+1+1=f(1)+2=f(0)+1+2=f(0)+3=0+3=3,
解:由f(x)的表达式得f(3)=f(2)+1=f(1)+1+1=f(1)+2=f(0)+1+2=f(0)+3=0+3=3,
当1≤x<2时,0≤x-1<1,
此时f(x)=f(x-1)+1=-3(x-1)2+4(x-1)+1=-3x2+10x-6,
当2≤x<3时,1≤x-1<2,则f(x)=f(x-1)+1=-3(x-1)2+10(x-1)-6+1=-3x2+16x-18,
作出函数f(x)的图象如图:
若于x的方程f(x)=ax+1恰有三个不同的解,
则等价为函数f(x)与y=ax+1恰有三个不同的交点,
直线y=ax+1过定点D(0,1),
当直线过点C(1,1)时,此时a=0,直线和f(x)有2个交点,
当直线过点A(2,2)时,此时2=2a+1,解得a=$\frac{1}{2}$,此时直线和f(x)有4个交点,
当直线经过点B(3,3)时,即3=3a+1,解得a=$\frac{2}{3}$,
当直线y=ax+1与f(x)=-3x2+4x相切时,
即-3x2+4x=ax+1,
即3x2+(a-4)x+1=0,
由判别式△=(a-4)2-12=0,
解得a=4+2$\sqrt{3}$(此时直线的斜率a<$\frac{2}{3}$,不成立舍去)或a=4-2$\sqrt{3}$,
此时直线和f(x)有4个交点,
综上要使两个函数的图象恰有三个不同的交点,
则直线满足在DC和DA之间,或在切线和DB之间,
即0<a<$\frac{1}{2}$,或4-2$\sqrt{3}$<a<$\frac{2}{3}$.
即(0,$\frac{1}{2}$)∪(4-2$\sqrt{3}$,$\frac{2}{3}$).
故答案为:3,(0,$\frac{1}{2}$)∪(4-2$\sqrt{3}$,$\frac{2}{3}$).
点评 本题主要考查函数与方程的应用,利用分段函数作出函数的图象,利用数形结合是解决本题的关键.综合性较强,运算量较大,是个难题.

| A. | $\frac{29}{2}$ | B. | $\frac{21}{2}$ | C. | -$\frac{11}{2}$ | D. | $\frac{11}{2}$ |
| A. | y=x-1 | B. | y=ln(x+1) | C. | y=($\frac{1}{2}$)x | D. | y=x+$\frac{1}{x}$ |
| A. | $[-\frac{1}{3},0)∪(0,\frac{1}{3}]$ | B. | [-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-5,5] |

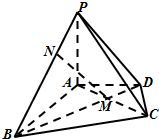 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.