题目内容
8.下列函数中,既是奇函数又存在极值的函数是( )| A. | y=x3 | B. | $y=x+\frac{1}{x}$ | C. | y=x•e-x | D. | y=ln(-x) |
分析 判断A没有极值,C,D不是奇函数,判断推出结果.
解答 解:由选项可知,A选项y=x3单调递增(无极值),C、D选项不是奇函数,
函数$y=x+\frac{1}{x}$满足f(-x)=-f(x),函数是奇函数,
x>0时,$y=x+\frac{1}{x}≥2$,当且仅当x=1时取得最小值,x>0时有极小值.
同理可得,当x<0时,$y=x+\frac{1}{x}$≤-2,当且仅当x=-1时取得最大值,也是极大值.
即B选项既为奇函数又存在极值.
故选:B.
点评 本题考查函数的奇偶性,函数的极值,考查计算能力.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
18.若x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )
| A. | $\frac{11}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
13.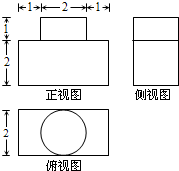 如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
 如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )| A. | 8+π | B. | 8+4π | C. | 16+π | D. | 16+4π |
 如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围为[-$\sqrt{2}$,$\sqrt{2}$].
如图,已知点P(2,0),且正方形ABCD内接于⊙O:x2+y2=1,M、N分别为边AB、BC的中点.当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围为[-$\sqrt{2}$,$\sqrt{2}$].
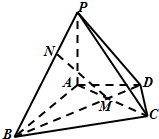 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.