题目内容
8.已知双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的一条渐近线与$y=\sqrt{3}x-1$平行,且它的一个焦点在抛物线x2=24y的准线上,则双曲线的方程为( )| A. | $\frac{y^2}{36}-\frac{x^2}{108}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{108}-\frac{x^2}{36}=1$ | D. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ |
分析 求出抛物线的准线方程,可得双曲线的焦点,即有c=6,再由渐近线方程可得a,b的方程,解出a,b,进而得到双曲线的方程.
解答 解:由题意可得,抛物线x2=24y的准线为y=-6,
双曲线的一个焦点为(0,-6),即有c=6,
又双曲线$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1({a>0,b>0})$的一条渐近线与$y=\sqrt{3}x-1$平行,
∴$\frac{a}{b}=\sqrt{3}$,36=a2+b2=4b2,b2=9,a2=27,
则所求双曲线的方程为$\frac{{y}^{2}}{27}-\frac{{x}^{2}}{9}=1$.
故选:D.
点评 本题考查抛物线和双曲线的方程和性质,考查渐近线方程的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
19.已知两点M(-1,0),N(1,0),若直线y=k(x-2)上存在点P,使得PM⊥PN,则实数k的取值范围是( )
| A. | $[-\frac{1}{3},0)∪(0,\frac{1}{3}]$ | B. | [-$\frac{\sqrt{3}}{3}$,0)∪(0,$\frac{\sqrt{3}}{3}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-5,5] |
3.数列1,3,7,13,…的第6项为( )
| A. | 21 | B. | 19 | C. | 31 | D. | 29 |
13.一个算法的程序框图如图所示,该程序输出的结果为( )


| A. | $\frac{36}{55}$ | B. | $\frac{10}{11}$ | C. | $\frac{5}{11}$ | D. | $\frac{72}{55}$ |
20.i是虚数单位,复数$\frac{-1+2i}{3+4i}$=( )
| A. | $\frac{1}{5}+\frac{2}{5}i$ | B. | $-\frac{1}{5}+\frac{2}{5}i$ | C. | 1-2i | D. | -1-2i |
17.为了比较两种复合材料制造的轴承(分别称为类型I轴承和类型II轴承)的使用寿命,检验了两种类型轴承各30个,它们的使用寿命(单位:百万圈)如下表:
类型I
(Ⅰ)根据两组数据完成下面茎叶图;
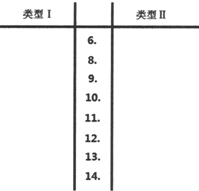
(Ⅱ)分别估计两种类型轴承使用寿命的中位数;
(Ⅲ)根据茎叶图对两种类型轴承的使用寿命进行评价.
类型I
| 6.2 | 6.4 | 8.3 | 8.6 | 9.4 | 9.8 | 10.3 | 10.6 | 11.2 | 11.4 | 11.6 | 11.6 | 11.7 | 11.8 | 11.8 |
| 1 12.2 | 12.3 | 12.3 | 12.5 | 12.5 | 12.6 | 12.7 | 12.8 | 13.3 | 13.3 | 13.4 | 13.6 | 13.8 | 14.2 | 14.5 |
| 类型II | ||||||||||||||
| 1 8.4 | 8.5 | 8.7 | 9.2 | 9.2 | 9.5 | 9.7 | 9.7 | 9.8 | 9.8 | 10.1 | 10.2 | IO.3 | 10.3 | 10.4 |
| 1 10.6 | 10.8 | 10.9 | 11.2 | 11.2 | 11.3 | 11.5 | 11.5 | 11.6 | 11.8 | 12.3 | 12.4 | 12.7 | 13.1 | 13.4 |

(Ⅱ)分别估计两种类型轴承使用寿命的中位数;
(Ⅲ)根据茎叶图对两种类型轴承的使用寿命进行评价.
16.设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)与直线y=3的交点的横坐标构成以π为公差的等差数列,且x=$\frac{π}{6}$是f(x)的一条对称轴,则下列区间中不是函数f(x)的单调递增区间的是( )
| A. | [-$\frac{π}{3}$,0] | B. | [-$\frac{4π}{3}$,-$\frac{5π}{6}$] | C. | [$\frac{2π}{3}$,$\frac{7π}{6}$] | D. | [-$\frac{5π}{6}$,-$\frac{π}{3}$] |
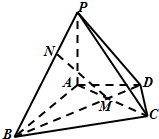 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$.